70 서포트 벡터 머신 이론
서포트 벡터 머신(Support Vector Machine)은 기계학습의 분야 중 하나로 정답 데이터가 있는 지도학습에 해당하는 부분.
서포트 벡터 머신도 신경망처럼 분류와 수치예측(회귀)을 위해 사용.
두 개의 군집(class)이 주어졌을 때 SVM 알고리즘은 주어진 데이터 집합을 바탕으로 하여 새로운 데이터가 어느 군집(class)에 속할 지를 판단하는 선형 분류 모델을 생성함. 선형분류와 더불어 비선형 분류에서도 사용됨.
ㅇ 서포트 벡터 머신의 결정경계


결정경계란 분류를 위한 기준선. 2차원일 때는 선이고 3차원 일때는 평면.
우리가 생각할 수 있는 부분은 3차원까지이고 차원이 더 많아지게 되면 평면이 아닌 초평면이 됨.
ㅇ그렇다면, 아래에서 데이터를 가장 잘 분류한 결정경계는 무엇인가?
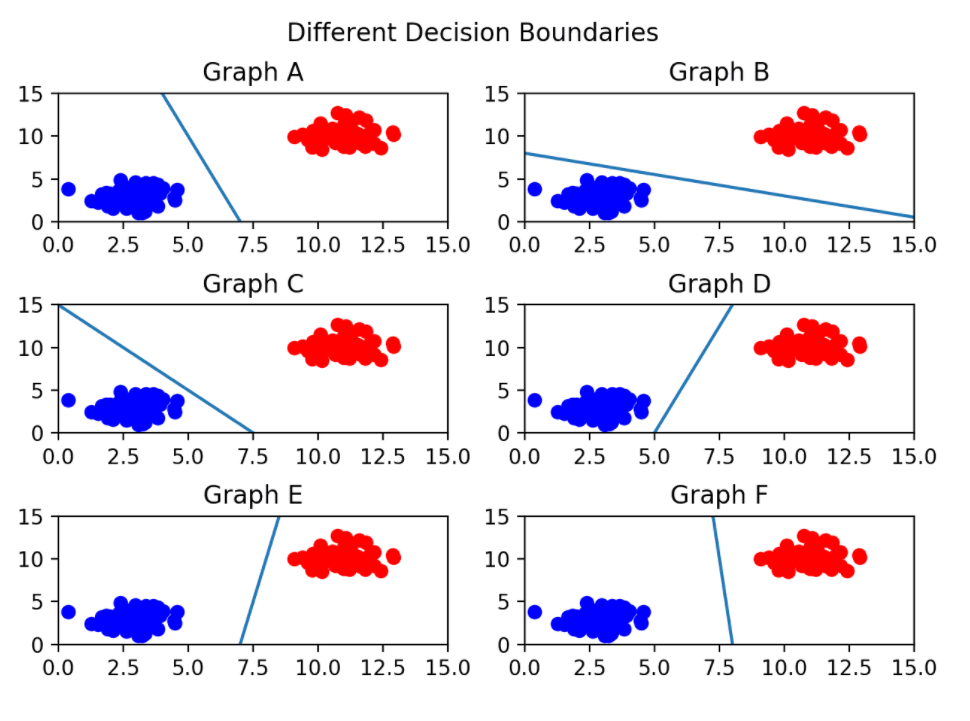
ㅇ서포트 벡터머신에서 서포트 벡터는 무엇인가?
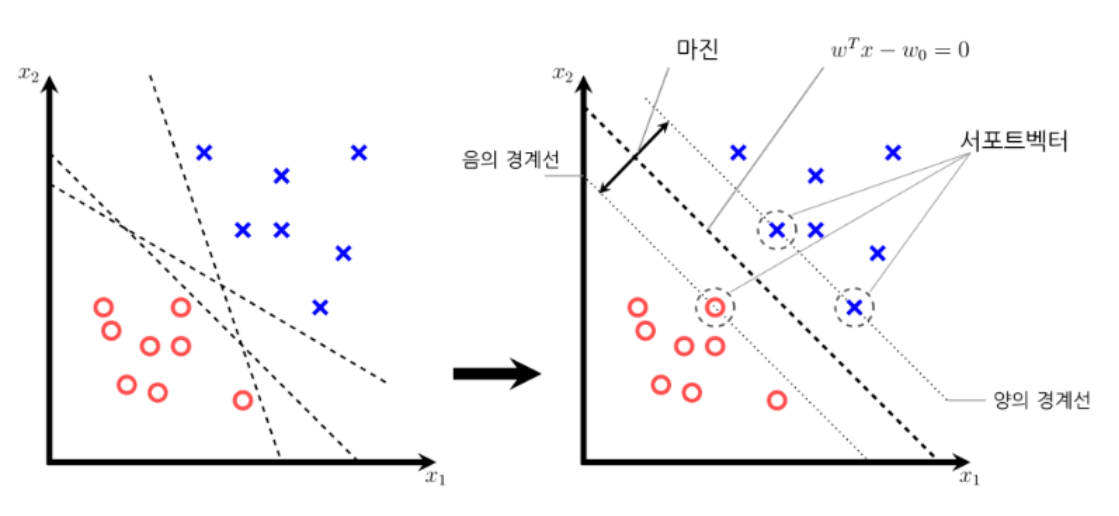
서포트 벡터는 결정경계와 가까이 있는 데이터 포인트들을 의미. 이 데이터들이 경계를 정의하는 결정적인 역할을 함.
ㅇ마진이란?
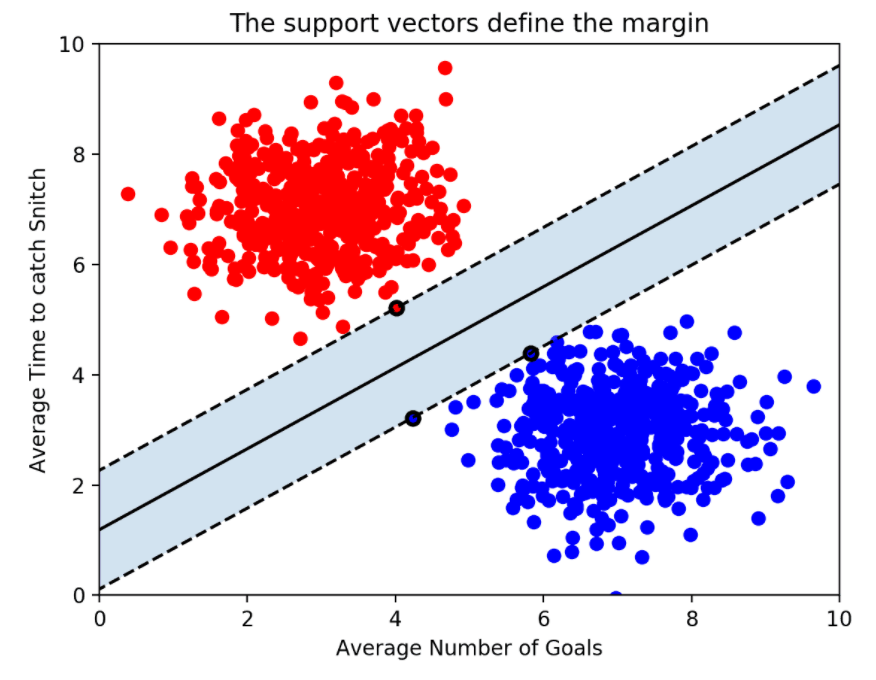
양의 경계선과 음의 경계선의 거리를 마진이라고 함 > 마진을 최대화하는 결정경계를 찾는게 서포트 벡터 머신의 목표
최적의 결정경계 = 마진 최대화
ㅇ 소프트마진, 하드마진

> 하드마진은 이상치까지 서포트벡터로 설정하여 완벽하게 분리를 해냈으나 오버피팅이 될 수 있음. 서포트 벡터와 결정경계 사이의 거리가 매우 좁아져서 마진이 작아짐.(언더피팅↓, 오버피팅↑)
> 소프트 마진은 이상치들이 마진 안에 어느정도 포함되도록 너그럽게 기준을 잡음. 서포트 벡터와 결정경계의 거리가 멀어져서 오버피팅 문제를 줄일 수 있음. 대신 언더피팅 문제 발생(언더피팅↑, 오버피팅↓)
ㅇ이런 오류를 어느정도 허용하는지 결정하는 하이퍼 파라미터


> c는 클수록 하드마진(오류를 허용하지 않음) , 작을수록 소프트 마진(오류 허용)이 일어남
> gamma는 결정경계를 얼마나 유연하게 그을 것인지 정해주는 것. gamma를 높이면 학습 데이터에 많이 의존하게 되어 결정경계를 구불구불하게 긋게 됨. (오버피팅 초래)
반대로 gamma를 낮추면 학습 데이터에 별로 의존하지 않고 결정경계를 긋게 되므로 오버피팅은 줄일 수 있지만 언더피팅이 발생할 수 있음.
하이퍼 파라미터 최적화(r - caret, 파이썬 - gridsearch)를 사용해서 적절한 파라미터를 찾으면 됨.
ㅇ로지스틱회귀와 서포트 벡터 머신의 성능 차이를 파이썬으로 실험하기
- 로지스틱 회귀 분류 1
#1. 데이터 생성
#2. 로지스틱 회귀모델 생성
#3. 모델 훈련
#4. 훈련 데이터를 어떻게 분류했는지 시각화
#1. 데이터 생성
from sklearn.datasets import make_blobs
x,y = make_blobs(centers = 2, random_state = 8)
import mglearn
import matplotlib.pyplot as plt
mglearn.discrete_scatter(x[:,0], x[:,1], y)
plt.xlabel("feature 0")
plt.ylabel("feature 1")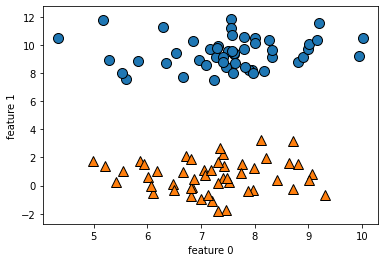
#4. 모델이 훈련 데이터를 어떻게 분류했는지 시각화 하기
mglearn.plots.plot_2d_separator(model, x) #결정경계선 출력
mglearn.discrete_scatter(x[:,0], x[:,1], y) #산포도 그래프 출력
plt.xlabel("feature 0")
plt.ylabel("feature 1")
plt.show()
#5. 정확도 확인
model.score(x,y) # 1
- 로지스틱 회귀 분류 2
#1. 데이터 생성
#2. 로지스틱 회귀모델 생성
#3. 모델 훈련
#4. 훈련 데이터를 어떻게 분류했는지 시각화
#1. 데이터 생성
from sklearn.datasets import make_blobs
x,y = make_blobs(centers = 4, random_state = 8)
y = y%2 #4개의 군집을 2개의 군집으로 변경하기 위함
import mglearn
import matplotlib.pyplot as plt
mglearn.discrete_scatter(x[:,0], x[:,1], y)
plt.xlabel("feature 0")
plt.ylabel("feature 1")
#2. 로지스틱 회귀 모델 생성
from sklearn.linear_model import LogisticRegression
model2 = LogisticRegression()
#3. 모델훈련
model2.fit(x,y)
#4. 모델이 훈련 데이터를 어떻게 분류했는지 시각화 하기
mglearn.plots.plot_2d_separator(model2, x) #결정경계선 출력
mglearn.discrete_scatter(x[:,0], x[:,1], y) #산포도 그래프 출력
plt.xlabel("feature 0")
plt.ylabel("feature 1")
plt.show()
#5. 정확도 확인
model2.score(x,y) #0.65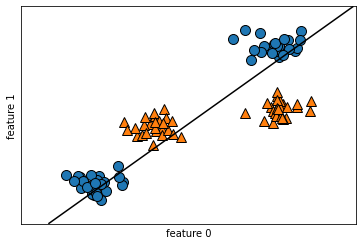
> 선으로 분류하기 어려운 데이터를 로지스틱 회귀 모델에 주었더니 정확도가 0.65 나오면서 분류를 제대로 하지 못함.
성능을 개선하려면 다음의 하이퍼 파라미터를 조정해줘야함.
solvers(경사하강법) = ['newton-cg','lbfgs','liblinear']
c_values = [100,10,1.0, 0.1, 0.01]
==> 하지만, 이 데이터에서는 LogisticRegression()의 하이퍼 파라미터를 조정해도 분류를 여전히 못함. 결정경계가 바뀌지 않음.
따라서 이 같은 데이터를 분류할 때는 서포트 벡터 머신으로 모델을 변경하면 분류할 수 있음.
- 로지스틱 회귀 분류 3 : 서포트 벡터 머신
#6. 성능개선
#서포트 벡터 머신 모델 생성
from sklearn.svm import SVC
model3 = SVC()
model3.fit(x,y)
#시각화
mglearn.plots.plot_2d_separator(model3, x, fill = True, alpha = 0.3) #결정경계선 출력
mglearn.discrete_scatter(x[:,0], x[:,1], y) #산포도 그래프 출력
plt.xlabel("feature 0")
plt.ylabel("feature 1")
plt.show()
model3.score(x,y) # 1
문제359. (점심시간 문제) 지금 위의 어려운 데이터를 서포트 벡터 머신으로 분류한 시각화 결과를 올리시오
(위의 문제358번 코드랑 동일함)
- 로지스틱 회귀 분류 4 : 서포트 벡터 머신(하이퍼 파라미터 C)
6개의 군집을 만들어서 각각 3개씩을 1과 0으로 만들어서 분류하기
#1. 데이터 생성
from sklearn.datasets import make_blobs
x,y = make_blobs(centers = 6, random_state = 8)
y = ( y >= 3).astype(int)
import mglearn
import matplotlib.pyplot as plt
mglearn.discrete_scatter(x[:,0], x[:,1], y)
plt.xlabel("feature 0")
plt.ylabel("feature 1")
#서포트 벡터 머신 분류
from sklearn.svm import SVC
model4 = SVC()
model4.fit(x,y)
#시각화
mglearn.plots.plot_2d_separator(model4, x, fill = True, alpha = 0.3) #결정경계선 출력
mglearn.discrete_scatter(x[:,0], x[:,1], y) #산포도 그래프 출력
plt.xlabel("feature 0")
plt.ylabel("feature 1")
plt.show()
model4.score(x,y) #0.99
> 결정경계에 1개가 걸쳐있어서 정확도가 100%가 나오지 못하고 99%가 나옴. 분류하지 못한 훈련 데이터 하나를 악착같이 분류해내려면 서포트 벡터 머신의 하이퍼 파라미터인 C를 조정하면 됨.
# 서포트 벡터 머신 - 하이퍼 파라미터 C 조정
from sklearn.svm import SVC
model5 = SVC(C = 10)
model5.fit(x,y)
#시각화
mglearn.plots.plot_2d_separator(model5, x, fill = True, alpha = 0.3) #결정경계선 출력
mglearn.discrete_scatter(x[:,0], x[:,1], y) #산포도 그래프 출력
plt.xlabel("feature 0")
plt.ylabel("feature 1")
plt.show()
model5.score(x,y) # 1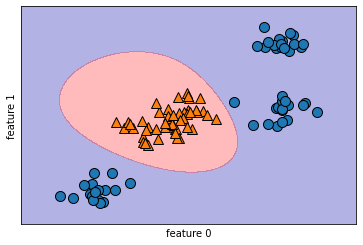
> C가 커지는 대신 마진은 작아짐
- 로지스틱 회귀 분류 5 : 서포트 벡터 머신(하이퍼 파라미터 C, gamma)
#1. 데이터 생성
from sklearn.datasets import make_blobs
x,y = make_blobs(centers = 6, random_state = 8)
y = y%2
import mglearn
import matplotlib.pyplot as plt
mglearn.discrete_scatter(x[:,0], x[:,1], y)
plt.xlabel("feature 0")
plt.ylabel("feature 1")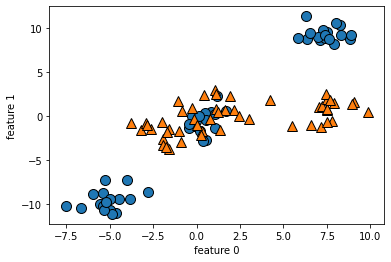
# 서포트 벡터 머신 - 하이퍼 파라미터 C = 10
from sklearn.svm import SVC
model6 = SVC(C = 10)
model6.fit(x,y)
#시각화
mglearn.plots.plot_2d_separator(model6, x, fill = True, alpha = 0.3) #결정경계선 출력
mglearn.discrete_scatter(x[:,0], x[:,1], y) #산포도 그래프 출력
plt.xlabel("feature 0")
plt.ylabel("feature 1")
plt.show()
model6.score(x,y) # 0.84
# 서포트 벡터 머신 - 하이퍼 파라미터 C = 10, gamma = 5
from sklearn.svm import SVC
model6 = SVC(C = 10, gamma = 5)
model6.fit(x,y)
#시각화
mglearn.plots.plot_2d_separator(model6, x, fill = True, alpha = 0.3) #결정경계선 출력
mglearn.discrete_scatter(x[:,0], x[:,1], y) #산포도 그래프 출력
plt.xlabel("feature 0")
plt.ylabel("feature 1")
plt.show()
model6.score(x,y)
분류하기 쉬운 데이터에서는 C만 써서 분류할 수 있는데 분류하기 어려운 데이터(데이터가 중첩되어 있고 섞여있는 경우)는 C만으로 분류가 안됨. 이때 gamma를 써서 분류하면 됨.
독립변수의 갯수가 많으면 4차원 이상이 되기 때문에 머릿속으로 분류하는게 상상되지 않음. C와 gamma를 같이 사용해서 정확도를 올리면 됨.
적절한 하이퍼 파라미터의 조합을 for문으로 하나씩 돌려서 알아내는데는 한계가 있음
> R의 caret 패키지와 파이썬의 gridsearch를 이용해서 알아내면 편하게 알아낼 수 있음
'Study > class note' 카테고리의 다른 글
| 머신러닝 / 파이썬으로 서포트 벡터 머신 모델 만들기 (0) | 2022.02.24 |
|---|---|
| 머신러닝 / R로 서포트 벡터 머신 모델 만들기 (0) | 2022.02.23 |
| 머신러닝 / R 로 신경망 모델 만들기(분류), 파이썬으로 신경망 모델 만들기(분류) (0) | 2022.02.22 |
| 머신러닝 / 하이퍼 파라미터 최적화(grid search), 파생변수 추가 (0) | 2022.02.22 |
| 머신러닝 / 파이썬으로 신경망 모델 만들기 (0) | 2022.02.21 |
