머신러닝 / 회귀분석(수치예측)
회귀분석은 하나의 변수가 나머지 다른 변수들과의 선형관계를 갖는가의 여부를 분석하는 방법으로 하나의 종속변수(예측하고자 하는 값)와 독립변수 사이의 관계를 명시하는 것을 말함.
ex. 집값에 가장 영향을 주는 요소가 무엇인가?
- 독립변수 : 종속변수에 영향을 주는 변수(평수, 역세권, 학군...)
- 종속변수 : 서로 관계를 가지고 잇는 변수등 중에서 다른 변수에 영향을 받는 변수(집값)

53 단순회귀분석 이론
ex.공부한 시간에 따른 시험 성적
x = [1,2,3] # 공부시간
y = [3,5,7] # 시험성적
x = 4일때, y값은?
> y = 2x + 1
데이터가 3개밖에 없어서 금방 y값을 추정하는 방정식을 사람이 손으로 구할 수 있었는데 만약에 데이터가 많고 식이 더 복잡해진다면, 사람이 알아내는 것보다는 컴퓨터가 알아내는게 더 나음. 컴퓨터가 위의 식을 알아내라고 하려면 가설을 세워야함.
H(W, b) = Wx + b (목표 : W = 2, b = 1)
가설 초기화
W = 1
b = 0

1번 직선에서 2번직선이 되도록 기계가 데이터를 학습해서 스스로 2번 직선의 방정식을 알아내려면 최소제곱 추정법을 사용해야함.
ㅇ최소 제곱 추정법(p257)
최적의 W(기울기)와 b(절편)을 결정하기 위해서는 최소제곱으로 알려진 추정기법을 사용해야함. 실제값과 예측값 사이의 수직 직선이 오차(잔차)를 제곱해서 구한 총합을 알아야함.


(Wxi + b: 예측값, yi = 실제값)
> 오차의 합을 최소화 하는 것 > 기계가 해결해야할 문제


> cost가 최소가 되는 지점의 w값(global minimum)을 알아내야함
기울기(W)와 절편(b)를 알아내는 방법?
1. 사람 --> 수학공식 이용
2. 기계 --> 경사하강법을 이용
- 수학공식을 이용했을 때
예제1. 어느 실험실에서 10시간, 20시간, 30시간, 40시간마다 물질의 방사능 수치를 측정한 자료가 있을 때 35시간에 물질의 방사능 수치는 얼마로 예측되는가?
x <- c(10,20,30,40)
y <- c(300,250,200,150)
W <- cov(x,y) / var(x) #x,y의 공분산 / x의 분산
W # -5
b <- mean(y) + 5 * mean(x)
b #350문제281. 단순회귀직선 y = -5x + 350. 그러면 시간이 25시간일때의 방사능 수치는 어떻게 되는가?
y <- W * x + b
x <- 35
y #175문제282.
# R
simple_regression <- function(x_num) {
x <- c(10, 20, 30,40)
y <- c(300, 250, 200, 150)
W <- cov(x,y) / var(x) # p259 기울기
b <- mean(y) - W * mean(x) # p258 절편
y_hat <- W*x_num + b
print(y_hat)
}
simple_regression(35)문제283. 탄닌 함유량과 애벌레의 성장간의 실험결과표를 이용해서 탄닌 함유량이 9일때 성장률이 어떻게 되는지 알기 위해 regression.txt를 R로 로드하시오.
reg <- read.table("c:\\data\\regression.txt", header = T) #텍스트파일 불러오는 방법, header = T 컬럼구성
reg> 탄닌함유량이 많을수록 성장률이 떨어지는 것을 관찰한 데이터
문제284. 위의 데이터로 산포도 그래프를 그리는데 x축을 탄닌함유량(tannin)으로 두고 y축을 애벌레 성장률(growth)로 해서 그리시오.
plot(growth ~ tannin, data = reg,pch=21, col = 'darkgreen', bg = 'darkgreen',cex=2 )
문제285. 탄닌 함유량(reg$tannin)과 애벌레의 성장률(reg$growth)을 가지고 회귀 직선의 방정식을 알아내서 탄닌 함유량이 9일때 애벌레 성장률 예측값을 출력하시오.
reg_func <- function(x_num) {
x <- reg$tannin
y <- reg$growth
W <- cov(x,y) / var(x)
b <- mean(y) - W * mean(x)
y_hat <- W*x_num + b
print(y_hat)
}
reg_func(9) #0.8055556문제286. 위의 함수를 파이썬으로 구현하시오.
import pandas as pd
import numpy as np
reg = pd.read_csv("c:\\data\\regression.txt",sep = '\t')
def reg_func(x_num):
x = reg['tannin']
y = reg['growth']
W = x.cov(y) / x.var() # 데이터프레임의 공분산과 분산 구하는 법
b = np.mean(y) - W * np.mean(x)
return W*x_num + b
reg_func(9) #0.8055555555555571+) 텍스트파일을 불러오는 또 다른 방법
reg2 = pd.read_table("c:\\data\\regression.txt")
문제287. 파이썬으로 탄닌 함유량과 애벌레 성장률간의 산포도 그래프를 그리시오.
# pandas
import pandas as pd
reg = pd.read_csv("c:\\data\\regression.txt",sep = '\t')
reg.plot(style = ".", x = "tannin", y = "growth", color = 'green')
+) 분산 계산할 때 자유도 차이
import numpy as np
print( np.var(reg2['tannin']) ) # 넘파이 자유도 default 0
import pandas as pd
x = reg2['tannin']
print( x.var() ) # 판다스 자유도 default 1
ㅇR함수 lm을 이용해서 단순회쉬 분석 실습
지금까지는 우리가 직접 기울기와 절편을 구하는 수학식을 코드로 구현한 것이고 지금부터는 lm함수를 이용해 기울기와 절편을 구해볼 것
데이터 : regression.txt
탄닌 함유량과 애벌레 성장간의 관계에 대한 회귀식 도출
#1. 데이터 로드
#2. 산포도 그래프
#3. 회귀분석을 해서 회귀계수인 기울기와 절편 구하기
#4. 2번에서 시각화한 산포도 그래프에 회귀직선을 겹쳐서 그림
#5. 그래프 제목을 회귀직선의 방정식으로 출력
# R
#1. 데이터 로드
reg <- read.table("c:\\data\\regression.txt", header = T)
#2. 산포도 그래프
attach(reg) #컬럼 앞에 알아서 데이터프레임 붙여줌 reg$tannin > tannin
plot(growth ~ tannin, data = reg, pch = 21, col = 'lightblue', bg = 'lightblue',cex=2)
#3. 회귀분석을 해서 회귀계수인 기울기와 절편 구하기
model <- lm(growth ~ tannin, data = reg)
modellm(종속변수명 ~ 독립변수명, data = 데이터프레임명)
Coefficients:
(Intercept) tannin
11.756 -1.217
> 절편 기울기
#4. 2번에서 시각화한 산포도 그래프에 회귀직선을 겹쳐서 그림
attach(reg) #컬럼 앞에 알아서 데이터프레임 붙여줌 reg$tannin > tannin
plot(growth ~ tannin, data = reg, pch = 21, col = 'lightblue', bg = 'lightblue',cex=2)
model <- lm(growth ~ tannin, data = reg)
abline(model, col = 'red')
#5. 그래프 제목을 회귀직선의 방정식으로 출력
title("y = -1.217 * x + 11.756 ")
문제288. 광고비가 매출에 미치는 영향조사를 위한 회귀분석 그래프를 그려주세요.
데이터 : simple_hg.csv
cost = 광고비, input = 매출액
#1. 데이터 로드
hg<- read.csv("c:\\data\\simple_hg.csv")
head(hg)
#2. 산포도 그래프
attach(hg)
plot(input ~ cost, data = hg, pch = 21, col = 'lightblue', bg = 'lightblue',cex=2)
#3. 회귀분석을 해서 회귀계수인 기울기와 절편 구하기
model <- lm(input ~ cost, data = hg)
model
#4. 2번에서 시각화한 산포도 그래프에 회귀직선을 겹쳐서 그림
plot(input ~ cost, data = hg, pch = 21, col = 'lightblue', bg = 'lightblue',cex=2)
model <- lm(input ~ cost, data = hg)
abline(model, col = 'red')
#5. 그래프 제목을 회귀직선의 방정식으로 출력
title("y = 2.186 * x + 62.929 ")
> 잔차까지 표현하는 코드
y_hat <- predict( model, cost= cost ) # input 매출액 예측값 출력
y_hat # 예측값 출력
join <- function(i) { # join 이라는 이름의 함수를 생성
lines( c( cost[i], cost[i] ), c( input[i], y_hat[i] ), col='blue') # 녹색 라인 그래프
}
sapply( 1:19, join ) # 1부터 19를 join 함수에 입력한다.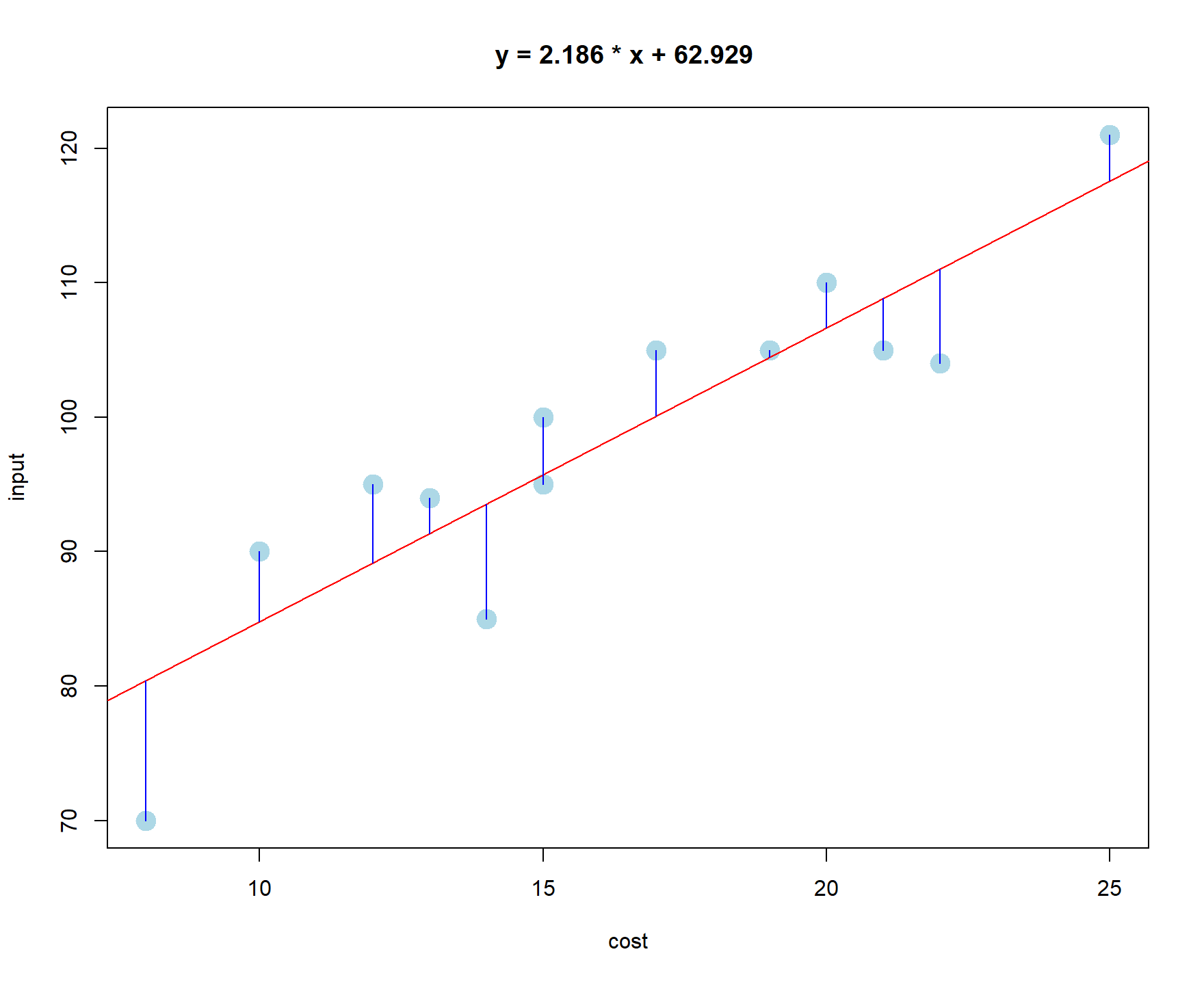
ㅇ오차와 잔차의 차이
오차 = 모집단에서 실제값이 회귀선과 비교했을 때의 차이(실제값과 예측값과의 차이)
잔차 = 표본에서 실제값이 회귀선과 비교했을 때의 차이(실제값과 예측값과의 차이)
문제289. 탄닌 함유량과 애벌레의 성장률에 대한 산포도 그래프와 회귀 직선 그래프를 이번에는 파이썬으로 그리시오.
# python
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
reg = pd.read_csv("c:\\data\\regression.txt",sep = '\t')
x = reg['tannin']
y = reg['growth']
sns.set_style('whitegrid')
plt.scatter(x,y,color = 'green')
sns.regplot(x = 'tannin', y = 'growth', data = reg, scatter = False, fit_reg = True, color = 'red') # 산포도 안보고 싶으면 scatter = False
plt.show()
+) 산점도에 만약 회귀직선을 보고 싶지 않다면 fit_reg = False를 넣으면됨. default는 True.
문제290. 광고비와 매출액에 대한 산포도 그래프와 회귀직선을 파이썬으로 그리시오
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
hg = pd.read_csv("c:\\data\\simple_hg.csv")
x = hg['cost']
y = hg['input']
sns.set_style('whitegrid')
plt.scatter(x,y,color = 'green')
sns.regplot(x = 'cost', y = 'input', data = hg, scatter = False, fit_reg = True, color = 'red') # 산포도 안보고 싶으면 scatter = False
plt.show()
문제291. 광고비와 매출액 간의 회귀직선의 기울기와 절편을 파이썬으로 구하시오.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
#1. 데이터 로드
hg = pd.read_csv("c:\\data\\simple_hg.csv")
#2. 독립변수와 종속변수 지정
x = hg[['cost']]
y = hg[['input']]
#3. 모델 생성
from sklearn.linear_model import LinearRegression
model = LinearRegression()
#4. 모델 훈련
model.fit(x , y)
#5. 기울기와 절편 구하기
print('기울기 : %0.8f'%model.coef_) # 2.18648985
print('절편 : %0.8f'%model.intercept_) # 62.92913386
#6. 그래프 그리기
sns.set_style('whitegrid')
plt.scatter(x,y,color = 'green')
sns.regplot(x = 'cost', y = 'input', data = hg, scatter = False, fit_reg = True, color = 'red') # 산포도 안보고 싶으면 scatter = False
plt.title('y = 2.18648985 * x + 62.92913386',size = 15)
plt.show()
LinearRegression()에는 항상 데이터프레임 형태로만 데이터를 입력해야함
문제293. 탄닌 함유량과 애벌레 성장률 간의 plot그래프와 회귀직선 그래프를 그리는데, 제목에 회귀직선 방적식을 넣으시오
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
#1. 데이터 로드
reg = pd.read_csv("c:\\data\\regression.txt", sep='\t')
#2. 독립변수와 종속변수 지정
x = reg[['tannin']]
y = reg[['growth']]
#3. 모델 생성
from sklearn.linear_model import LinearRegression
model = LinearRegression()
#4. 모델 훈련
model.fit(x , y)
#5. 기울기와 절편 구하기
print('기울기 : %0.8f'%model.coef_)
print('절편 : %0.8f'%model.intercept_)
sns.set_style('whitegrid')
plt.scatter(x,y,color = 'green')
sns.regplot(x = 'tannin', y = 'growth', data = reg, scatter = False, fit_reg = True, color = 'red') # 산포도 안보고 싶으면 scatter = False
plt.title('y = %0.8f * x + %0.8f'%(model.coef_,model.intercept_),size = 15)
plt.show()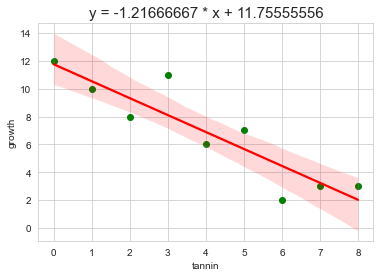
문제294. 위의 코드를 파이썬 데이터분석 자동화 코드에 19번에 넣으시오.
liner_reg = '''import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
#1. 데이터 로드
reg = pd.read_csv("c:\\data\\regression.txt", sep='\\t')
#2. 독립변수와 종속변수 지정
x = reg[['tannin']]
y = reg[['growth']]
#3. 모델 생성
from sklearn.linear_model import LinearRegression
model = LinearRegression()
#4. 모델 훈련
model.fit(x , y)
#5. 기울기와 절편 구하기
print('기울기 : %0.8f'%model.coef_)
print('절편 : %0.8f'%model.intercept_)
sns.set_style('whitegrid')
plt.scatter(x,y,color = 'green')
sns.regplot(x = 'tannin', y = 'growth', data = reg, scatter = False, fit_reg = True, color = 'red') # 산포도 안보고 싶으면 scatter = False
plt.title('y = %f * x + %f'%(model.coef_,model.intercept_),size = 15)
plt.show()
'''
문제295. (오늘의 마지막 문제) 자동화 코드 20번에 의사결정트리를 넣으시오.
tree = '''
# 1. 데이터 로드
import pandas as pd
wine = pd.read_csv("c:\\\data\\\wine.csv")
wine.shape #(178, 14)
wine.head() #Type컬럼이 label
# 2. 결측치 확인
wine.isnull().sum() #결측치 없음
# 3. 문자 데이터를 숫자로 변경
# 문자 데이터 없음
x = wine.iloc[:,1:]
y = wine.iloc[:,0]
# 4. 훈련 데이터와 테스트 데이터 분리
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size = 0.1, random_state = 1)
# 5. 훈련 데이터 정규화
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(x_train)
x_train2 = scaler.transform(x_train)
x_test2 = scaler.transform(x_test)
# print(x_train2.min(), x_train2.max()) #0.0 1.0000000000000002
# print(x_test2.min(), x_test2.max()) #-0.0326530612244898 0.9051355206847361
# 6. 의사결정트리 모델 생성
from sklearn.tree import DecisionTreeClassifier
model_wine = DecisionTreeClassifier(criterion = 'entropy', max_depth = 5, random_state = 1)
model_wine
# 7. 모델 훈련
model_wine.fit(x_train2, y_train)
# 8. 훈련된 모델로 테스트 데이터 예측
result_train = model_wine.predict(x_train2)
result_test = model_wine.predict(x_test2)
# 9. 모델 평가
train_pct = sum(result_train == y_train)/len(y_train) * 100
test_pct = sum(result_test == y_test)/len(y_test) * 100
print(train_pct, test_pct)
# from sklearn.metrics import confusion_matrix
# cross = confusion_matrix(y_test, result_test)
# cross
# 10. 모델 성능 개선
# 랜덤포레스트
from sklearn.ensemble import RandomForestClassifier
model_rd = RandomForestClassifier(n_estimators = 5, random_state = 1)
model_rd.fit(x_train2, y_train)
result_train = model_rd.predict(x_train2)
result_test = model_rd.predict(x_test2)
train_pct_rd = sum(result_train == y_train)/len(y_train) * 100
test_pct_rd = sum(result_test == y_test)/len(y_test) * 100
print(train_pct_rd, test_pct_rd)
# 11. 모델 시각화
from sklearn.tree import plot_tree #의사결정트리를 그리는 모듈
from sklearn import tree #의사결정트리 모듈
import matplotlib.pyplot as plt
plt.figure(figsize = (12,12))
tree.plot_tree(model, filled = True, rounded = True) #filled = True하면 색깔이 표시됨
#rounded = True는 반올림
#plt.savefig('c:\\\data\\\tree_visualization.jpg') #저장
plt.show()'''