머신러닝 / 퍼셉트론 R과 파이썬으로 구현하기

ㅇ퍼셉트론(perceptron) --> "뇌세포 하나를 수학적으로 재현함"

     ㄴ 지각하다, 인지하다

기계를 학습시키려면 공부할 데이터(문제집과 답)를 줘야함.

AND 게이트			OR 게이트			Nand 게이트			Xor 게이트 (eXclusive or 게이트)
x1	x2	y	x1	x2	y	x1	x2	y	x1	x2	y
F(0)	F(0)	0	F(0)	F(0)	0	F(0)	F(0)	1	F(0)	F(0)	0
F(0)	T(1)	0	F(0)	T(1)	1	F(0)	T(1)	1	F(0)	T(1)	1
T(1)	F(0)	0	T(1)	F(0)	1	T(1)	F(0)	1	T(1)	F(0)	1
T(1)	T(1)	1	T(1)	T(1)	1	T(1)	T(1)	0	T(1)	T(1)	0

 

 

 

 

ㅇand게이트 퍼셉트론 R로 구현하기

예제1. 아래의 행렬을 만들고 inputs라는 변수에 넣으시오.

# R
inputs <- matrix(c(0,0,1,0,0,1,1,1), nrow = 4, ncol = 2, byrow = T)
inputs

예제2. 아래의 행렬을 만들고 targets라는 변수에 넣으시오.

targets <- matrix(c(0,0,0,1), nrow = 4, ncol = 1, byrow = T)
targets

예제3. 아래의 가중치 행렬을 w라는 이름으로 생성하시오.

w <- matrix(c(0.3, 0.4, 0.1), nrow = 3)
w

예제4. 아래의 행렬을 만들고 x0이라는 변수에 담으시오.

x0 <- matrix(c(-1,-1,-1,-1), nrow = 4)
x0

예제5. inputs행렬과 x0행렬을 cbind를 이용해 서로 붙여서 new_inputs 변수에 담으시오.

new_inputs <- cbind(x0,inputs)
new_inputs

예제6. new_inputs와 w행렬과의 곱을 구하시오.

k <- new_inputs %*% w
k

예제7. 위에서 작성한 inputs, targets, x0, new_inputs코드를 가지고 아래의 and_pcn함수를 생성하시오.

inputs <- matrix(c(0,0,1,0,0,1,1,1), nrow = 4, ncol = 2, byrow = T)
targets <- matrix(c(0,0,0,1), nrow = 4, ncol = 1, byrow = T)
x0 <- matrix(c(-1,-1,-1,-1), nrow = 4)
new_inputs <- cbind(x0,inputs)

and_pcn <- function(ni){
  w <- matrix(c(0.3, 0.4, 0.1), nrow = 3)
  for (i in (1:nrow(ni))){
    k <- ni[i, ] %*% w
    print(k)
  }
}
and_pcn(new_inputs)

예제8. 위에서 출력되고 있는 k값이 0보다 크면 1, 0보다 작거나 같으면 0이 출력되도록 코드를 수정하시오.

and_pcn <- function(ni){
  w <- matrix(c(0.3, 0.4, 0.1), nrow = 3)
  for (i in (1:nrow(ni))){
    k <- ni[i, ] %*% w
    k_prime <- ifelse(k>0, 1, 0)
    print(k_prime)
  }
}
and_pcn(new_inputs)

예제9.  위에서 출력되고 있는 k_prime(예측값)과 정답(targets)과의 차이인 오차가 출력되게끔 코드를 수정하시오.

and_pcn <- function(ni, t){
  w <- matrix(c(0.3, 0.4, 0.1), nrow = 3)
  for (i in (1:nrow(ni))){
    k <- ni[i, ] %*% w
    k_prime <- ifelse(k>0, 1, 0)
    cost <- t[i,] - k_prime
    
    print(cost)
  }
}
and_pcn(new_inputs, targets)

예제10. 비용(cost) 또는 오차가 0이 아니면 (즉, 오차가 생기면) 가중치 w0, w1, w2의 변화가 일어나게끔 코드를 구현하시오.

and_pcn <- function(ni, t){
  w <- matrix(c(0.3, 0.4, 0.1), nrow = 3)
  for (i in (1:nrow(ni))){
    k <- ni[i, ] %*% w
    k_prime <- ifelse(k>0, 1, 0)  # 활성화 함수(계단함수)
    cost <- t[i,] - k_prime  # 비용(오차)함수
    if(cost != 0){
      for (j in 1:nrow(w)){
        w[j] <- w[j]+0.05 * ni[i,j]*cost
      }
    }
  }
  print(w)
}

and_pcn(new_inputs, targets)

예제11. 가중치의 변화가 없을 때 위의 for루프문으로 반복하는 작업이 중단되면서 가중치가 출력되게 하시오.

아래의 전체 for문이 계속 반복되도록 하시오 = 무한루프

inputs <- matrix(c(0,0,1,0,0,1,1,1), nrow = 4, ncol = 2, byrow = T)
targets <- matrix(c(0,0,0,1), nrow = 4, ncol = 1, byrow = T)
x0 <- matrix(c(-1,-1,-1,-1), nrow = 4)
new_inputs <- cbind(x0,inputs)

and_pcn <- function(ni, t){
  w <- matrix(c(0.3, 0.4, 0.1), nrow = 3)
  for (i in (1:4)){  
    for (i in (1:nrow(ni))){
      k <- ni[i, ] %*% w
      k_prime <- ifelse(k>0, 1, 0)  # 활성화 함수(계단함수)
      cost <- t[i,] - k_prime  # 비용(오차)함수
      if(cost != 0){
        for (j in 1:nrow(w)){
          w[j] <- w[j]+0.05 * ni[i,j]*cost
        }
      }
    }
    print(w)
  }
}

and_pcn(new_inputs, targets)

 

 

ㅇ파이썬으로 and 퍼셉트론 구현하기

예제1. inputs 변수를 행렬로 만드시오.

#python
import numpy as np

inputs = np.array([0,0,1,0,0,1,1,1]).reshape(4,2)

예제2. targets 변수를 행렬로 만드시오.

targets = np.array([0,0,0,1]).reshape(4,1)

예제3. 가중치 행렬 w를 만드시오.

w = np.array([0.3, 0.4, 0.1]).reshape(3,1)

예제4. x0 행렬을 만드시오.

x0 = np.array([-1,-1,-1,-1]).reshape(4,1)

예제5. inputs와 x0 행렬을 서로 붙여서 new_inputs라는 변수에 담으시오.

new_inputs = np.hstack((x0,inputs))

# 또는

new_inputs = np.column_stack((x0, inputs))

예제6. new_inputs(입력값)과 w(가중치) 행렬과의 곱을 구하시오.

k = np.dot(new_inputs, w)

예제7. 위의 결과를 출력하는 함수를 and_pcn이라는 함수로 아래와 같이 실행되게 하시오.

def and_pcn(ni, w):
    return np.dot(ni, w)
    
and_pcn(new_inputs, w)

예제8. 위에서 출력된 값이 0보다 크거나 같으면 1, 0보다 작으면 0을 출력하게끔 코드를 수정하시오.

def step_function(x):  #계단함수
    y = x >= 0
    
    return y.astype(np.int)  # y가 true = 1, false = 0

def and_pcn(ni, w):
    k = np.dot(ni, w)
    k_prime = step_function(k)
    
    return k_prime
    
and_pcn(new_inputs, w)

예제9. 위에서 출력된 결과(예상값)와 실제 정답(targets)과의 차이인 오차가 출력되게 코드를 수정하시오.

def step_function(x):  #계단함수
    y = x >= 0
    
    return y.astype(np.int)  # y가 true = 1, false = 0

def and_pcn(ni, w):
    k = np.dot(ni, w)
    k_prime = step_function(k)
    cost = targets - k_prime
    
    return cost
    
and_pcn(new_inputs, w)

예제10. 비용(cost) 또는 오차가 0이 아니면 가중치 w0,w1,w2의 변화가 일어나게끔 코드를 작성하시오. 그리고 가중치 3개를 출력하시오.

import numpy as np

inputs = np.array([0,0,1,0,0,1,1,1]).reshape(4,2)
targets = np.array([0,0,0,1]).reshape(4,1)
w = np.array([0.3, 0.4, 0.1]).reshape(3,1)
x0 = np.array([-1,-1,-1,-1]).reshape(4,1)
new_inputs = np.hstack((x0,inputs))

def step_function(x):  #계단함수
    y = x >= 0
    
    return y.astype(np.int)  # y가 true = 1, false = 0

def and_pcn(ni, w):
    targets = np.array([0,0,0,1]).reshape(4,1)
    
    for i in range(len(ni)):
        k = np.dot(ni[i,:], w)
        k_prime = step_function(k)
        cost = targets[i,:] - k_prime
        if cost != 0:
            for j in range(len(w)):
                w[j] = w[j] + 0.05 * ni[i,j] * cost
    
    
    print(w)
    
and_pcn(new_inputs, w)

 

=> step_function 함수 수정

: 파이썬의 부동소수점 오류로 인해 k값이 0으로 출력되지 않고 0에 근사한 값으로 출력되고 있음. 겉으로 보기엔 0이지만 포맷팅으로 전체 확인을 해보면 0에 근사한 값이 나옴. 따라서 부동소수점은 0보다 큰 값이 되므로 1이 출력됨.

np.round(x,2)로 코드를 수정해서 0.00으로 만들어야함. 

def step_function(x):  #계단함수
    y = np.round(x,2) >= 0
    
    return y.astype(np.int)  # y가 true = 1, false = 0

이때 y = np.round(x,2) >= 0 일때는 가중치가 0.4, 0.3, 0.1이 나오고, y = np.round(x,2) > 0 일때는 가중치가 0.35, 0.35, 0.1이 출력됨.

 

 

+) 지금까지의 코드를 전체 정리

import numpy as np

inputs = np.array([0,0,1,0,0,1,1,1]).reshape(4,2)  #and gate
targets = np.array([0,0,0,1]).reshape(4,1)  #정답
w = np.array([0.3, 0.4, 0.1]).reshape(3,1)  #가중치
x0 = np.array([-1,-1,-1,-1]).reshape(4,1)  #절편
new_inputs = np.hstack((x0,inputs))

def step_function(x):  #계단함수
    y = np.round(x,2) >= 0
    
    return y.astype(np.int)  # y가 true = 1, false = 0


def and_pcn(ni, w):
    targets = np.array([0,0,0,1]).reshape(4,1)  # and gate 정답
    
    for i in range(4):
        for i in range(len(ni)):
            k = np.dot(ni[i,], w)
            k_prime = step_function(k)
            cost = targets[i,] - k_prime
            if cost != 0:
                for j in range(len(w)):
                    w[j] = w[j] + 0.05 * ni[i,j] * cost
                    
        print(w)

    
and_pcn(new_inputs, w)

 

 

ㅇ활성화 함수의 종류 p318

뉴런에 입력되는 신호를 다음 신로호 보낼지 말지를 결정하는 함수(like 역치, 임계치)

현상 ---> 인문학자 : 발견 ---> 수학자 : 수학적 풀이 ---> 컴퓨터 과학자 : 코드로 완성

1. 계단함수 : 입력신호의 총합이 임계치를 넘느냐 안넘느냐를 숫자1과 0으로 리턴하는 함수

   ex :  f(0.3) = 1, f(-0.2) = 0

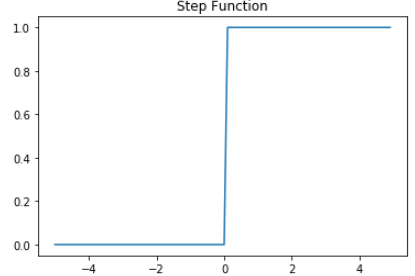
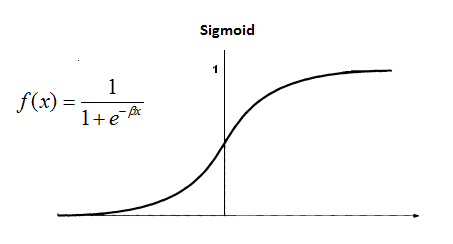
2. 시그모이드 함수 : 계단함수는 무조건 0 아니면 1을 리턴하지만 시그모이드 함수는 0~1 사이의 연속적인 실수값을 리턴함. 

단층 신경망(계단함수) : 입력층 ---> 출력층

다층 신경망(시그모이드) : 입력층 ---> 은닉층 ---> 출력층

 

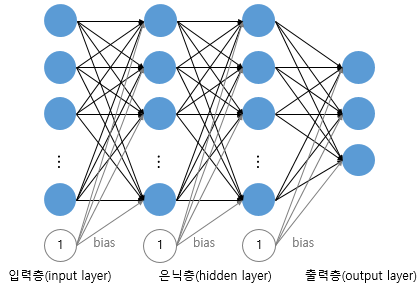
신경망을 단층이 아니라 다층 신경망을 사용하려면 활성화 함수를 sigmoid함수를 사용해야 함.

시그모이드 함수의 문제점? 기울기 소실 문제가 발생해서 신경망 학습이 제대로 안되는 문제가 생김.

> 가중치가 제대로 갱신이 안되어서 분류를 못함 > 시그모이드 함수의 단점을 개선하고자 렐루함수 생김.

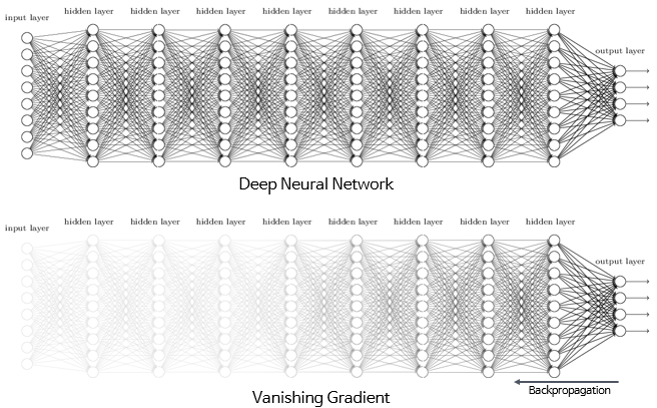
3. 렐루함수(Rectified Linear unit) 함수 : 입력값이 0보다 크면 그 값을 그 값을 그대로 출력하고 0 보다 작거나 같으면 0으로 출력하는 함수

 

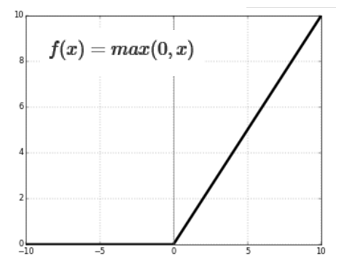
예제1. 활성화 함수인 계단함수를 R로 생성하고 계단함수 그래프를 그리시오(p.319)

#R
step <- function(x){ifelse(round(x,2)>=0, 1, 0)}
step(-0.1)
step(1.4)

x <- seq(-5,5, 0.01)  # -5 ~ 5까지 0.001 간격으로 출력
x

plot(x,step(x), col = 'blue',type = 'o', cex = 0.5)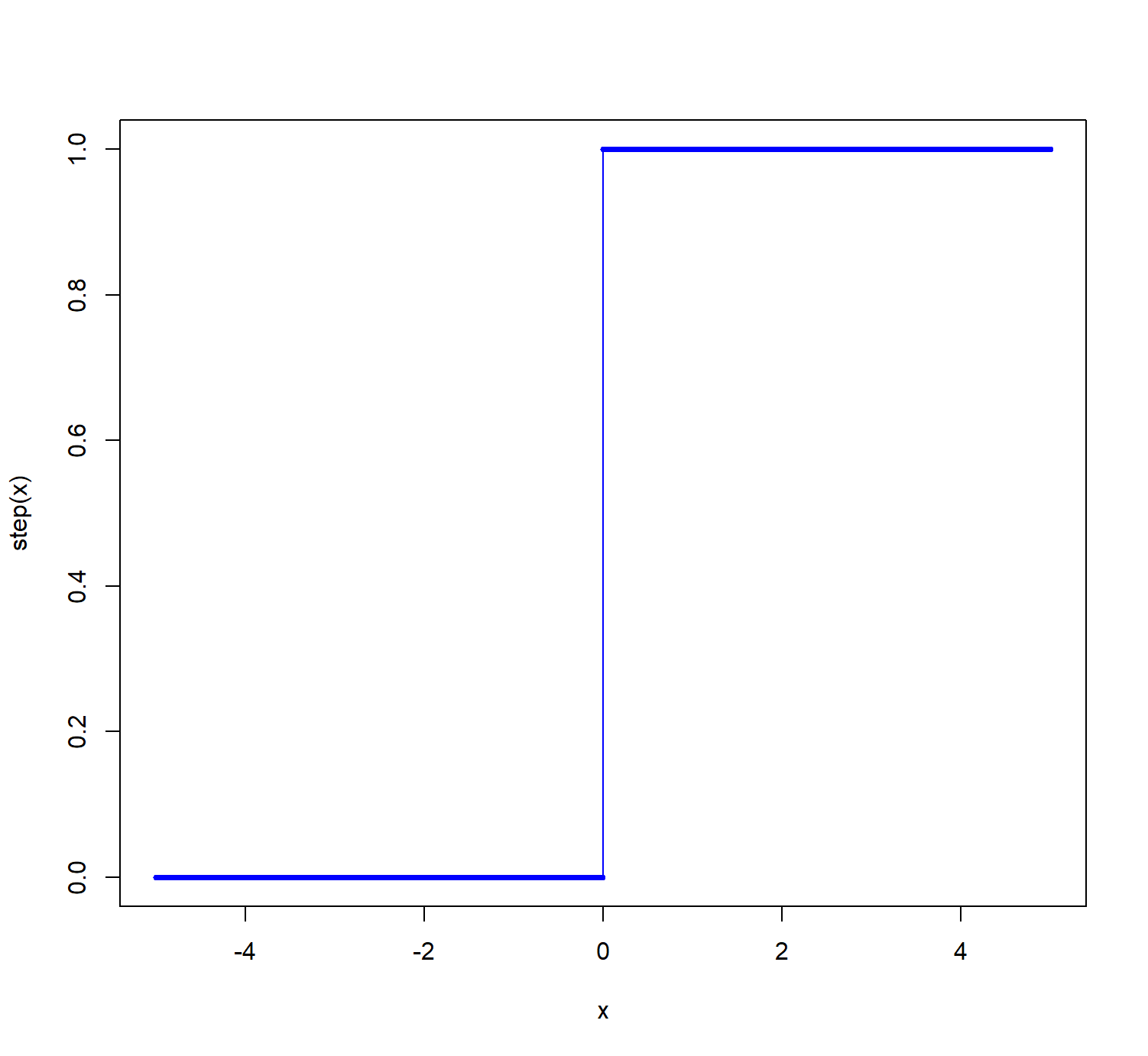

문제328. 이번에는 파이썬으로 계단함수를 만들고 계단함수 그래프를 그리시오.

#python
import numpy as np
import matplotlib.pyplot as plt

def step_function(x):
    return np.array(x > 0, dtype = np.int)

step_function(-0.2)
step_function(0.3)

x = np.arange(-5.0, 5.0, 0.1) # -5 ~ 5까지 0.1 간격
y = step_function(x)

plt.plot(x,y)
plt.show()

 

문제329. R로 시그모이드 함수를 만드시오.

#R
sigmoid <- function(x){ 1/ (1+exp(-x)) }
sigmoid(3) 
sigmoid(2)

 

문제330. (오늘의 마지막 문제) or게이트 퍼셉트론 함수를 파이썬으로 생성하시오.

import numpy as np

inputs = np.array([0,0,1,0,0,1,1,1]).reshape(4,2)  #and gate
# targets = np.array([0,0,0,1]).reshape(4,1)  #정답
w = np.array([0.3, 0.4, 0.1]).reshape(3,1)  #가중치
x0 = np.array([-1,-1,-1,-1]).reshape(4,1)  #절편
new_inputs = np.hstack((x0,inputs))

def step_function(x):  #계단함수
    y = np.round(x,2) >= 0
    
    return y.astype(np.int)  # y가 true = 1, false = 0


def and_pcn(ni, w):
    targets = np.array([0,1,1,1]).reshape(4,1)  # or gate 정답
    
    for i in range(4):
        for i in range(len(ni)):
            k = np.dot(ni[i,], w)
            k_prime = step_function(k)
            cost = targets[i,] - k_prime
            if cost != 0:
                for j in range(len(w)):
                    w[j] = w[j] + 0.05 * ni[i,j] * cost
                    
        print(w)

    
and_pcn(new_inputs, w)