딥러닝 / 오차역전파, Affine 계층 구현
ㅇ역전파 1단계
시그모이드 함수의 계산 그래프




순전파일때는 x값이 필요하지만 역전파일때는 y값이 필요하므로 y로 치환함.
ㅇ역전파 2단계 - p.168
덧셈노드는 상류의 값을 여과없이 그대로 하류로 내려보내는게 전부
ㅇ역전파 3단계 - p.168

ㅇ역전파 4단계 - p.169
곱셈 노드의 역전파는 순전파일때 상대편쪽에서 보냈던 값을 곱해주는 것.
순전파일때는 입력값 x가 필요했지만 역전파일때는 y값이 필요하므로 x를 y로 치환해야 함.


지금까지 만든 계산 그래프로 구현한 계층 2가지
1. 렐루함수 계층
2. 시그모이드 함수 계층
--------------------------------------------------------
앞으로 구현할 것
3. Affine 계층
4. softmax 함수 계층
11 Affine 계층 구현하기
신경망 순전파때 수행하는 행렬의 내적을 기하학에서는 어파인(Affine) 변환이라고 함.
그래서 신경망에서 입력값과 가중치의 내적의 합에 바이어스를 더하는 층으 Affine 계층이라고 부르면서 구현함.
앞에서는 sigmoid와 relu의 forward, backward를 구현했는데
지금은 입력값과 가중치를 내적하고 바이어스를 더하는 Affine 계층의 forward, backward를 구현할 예정
지금까지의 계산그래프에서는 노드 사이에 'scala'값이 흘렀는데, 이에 반해 어파인 계층에서는 행렬 내적을 해야하므로 '행렬'이 흐름.


문제109. 책 175페이지에 나오는 Affine 클래스를 생성하시오.(forward 까지만 구현)
class Affine:
def __init__(self, W, b): #신경망에 필요한 가중치와 바이어스를 생성하는 함수
self.W = W #클래스를 가지고 객체화 시킬때 필요한 가중치를 self.W에 입력
self.b = b #클래스를 가지고 객체화 시킬때 필요한 가중치를 self.b에 입력
self.x = None #순전파때 입력값을 저장할 변수 생성
self.dW = None #역전파 할 때 계산된 가중치의 기울기를 담을 변수 생성
self.db = None #역전파 할 때 계산된 바이어스의 기울기를 담을 변수 생성
def forward(self, x): #입력값과 가중치를 내적하고 바이어스를 더하는 순전파 함수 생성
self.x = x #입력값 행렬이 self.x에 입력됨
out = np.dot(x, self.W) + self.b #입력값 행렬과 가중치를 내적하고 바이어스를 더해서 out변수에 할당
return out
문제110. 아래의 입력값 행렬과 가중치 행렬을 넣어서 순전파 값을 출력하시오.
import numpy as np
x = np.array([[1,2]])
W = np.array([1,3,5,2,4,6]).reshape(2,3)
b = np.array([[1,1,1]])
affine = Affine(W,b) #객체생성
affine.forward(x) #array([[ 6, 12, 18]])
ㅇAffine 계층의 역전파 구현하기 - p173
곱셈의 역전파는 순전파일때 상대편 쪽에서 보냈던 값을 곱하는게 곱셈의 역전파였는데 dot(내적)의 역전파는 순전파일대 상대편 쪽에서 보냈던 값을 내적하는게 dot(내적)의 역전파.
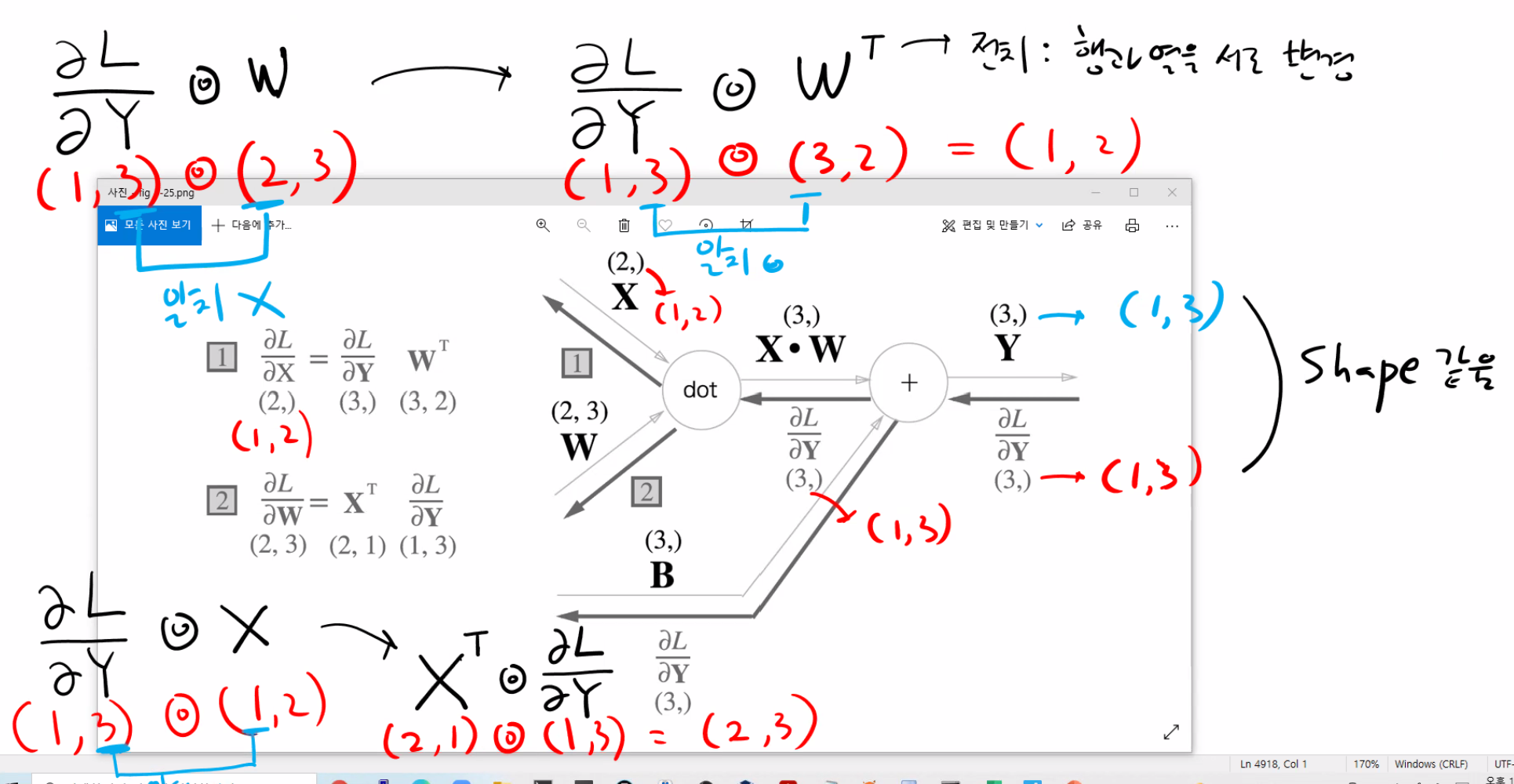
문제111. 위의 그림과 설명대로 Affine 계층 클래스의 backward 함수를 구현하시오.
class Affine:
def __init__(self, W, b): #신경망에 필요한 가중치와 바이어스를 생성하는 함수
self.W = W #클래스를 가지고 객체화 시킬때 필요한 가중치를 self.W에 입력
self.b = b #클래스를 가지고 객체화 시킬때 필요한 가중치를 self.b에 입력
self.x = None #순전파때 입력값을 저장할 변수 생성
self.dW = None #역전파 할 때 계산된 가중치의 기울기를 담을 변수 생성
self.db = None #역전파 할 때 계산된 바이어스의 기울기를 담을 변수 생성
def forward(self, x): #입력값과 가중치를 내적하고 바이어스를 더하는 순전파 함수 생성
self.x = x #입력값 행렬이 self.x에 입력됨
out = np.dot(x, self.W) + self.b #입력값 행렬과 가중치를 내적하고 바이어스를 더해서 out변수에 할당
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis = 0)
return dx
문제112. (점심시간 문제) 위의 Affine 클래스를 객체화 시켜서 아래의 입력값과 가중치 행렬값과 바이어스 값을 넣고 순전파를 실행한 후 아래의 오차인 dout 행렬을 이용해서 역전파된 결과를 출력하시오.
import numpy as np
x = np.array([[1,2]])
W = np.array([1,3,5,2,4,6]).reshape(2,3)
b = np.array([[1,1,1]])
dout = np.array([[2,2,1]])
affine = Affine(W,b) #객체생성
affine.forward(x) #array([[ 6, 12, 18]])
affine.backward(dout) #array([[13, 18]])
12 배치 단위용 Affine 계층 구현하기 - p.174
지금까지 구현한 Affine 계층은 입력 데이터를 아래와 같이 한 개만 입력했음.
x = np.array([[1,2]]) #(1,2)
mnist의 경우 이미지 한장은 (1,768).
컴퓨터를 이용해 이미지 한 장씩 학습 시키는 것은 너무 비효율적이고 시간이 오래걸림.
컴퓨터는 여러개의 이미지를 한 번에 학습시킬 수 있으므로, 다음과 같이 배치 단위로 학습해야함.
x = np.array([[1,2],[3,4],[4,1],[2,3],[9,1]]) #(5,2) <- 5장을 한 번에 신경망에 넣고 한번에 학습 시킴.
mnist의 경우 이미지 100장으로 (100,768) 로 입력하고, 설현 사진의 경우 100장으로 (32*32)으로 입력해야함.
그러면 Affin 계층의 클래스 설계도도 배치사이즈에 맞게 코드를 구현해야 함.
ㅇ배치 처리 전 입력데이터와 배치 처리 후 입력데이터를 각각 affine계층에 넣었을 때 어떤 결과가 출력되는지 확인
#배치 처리 전
x = np.array([[1,2]]) # 입력 데이터 1개
W = np.array([[1,3,5],[2,4,6]])
b = np.array([[1,1,1]])
dout = np.array([[2,2,1]])
affine1 = Affine(W, b) # 객체화
print(affine1.forward(x)) # array([[ 6, 12, 18]])
print(affine1.backward(dout))
# 배치 처리 후
x = np.array([ [1,2],[3,4],[4,1],[2,3],[9,1] ]) # (5,2) 5장을 한번에 신경망에 넣고 한번에 학습 시킵니다.
W = np.array([[1,3,5],[2,4,6]])
b = np.array([[1,1,1]])
dout = np.array([[2,2,1],[2,2,1],[1,5,2],[2,1,2],[1,2,6]]) #( 5,3 )
affine1 = Affine(W, b) # 객체화
print(affine1.forward(x)) # array([[ 6, 12, 18]])
print(affine1.backward(dout))
ㅇ배치 단위가 아닐때

ㅇ배치 단위일 때

class Affine:
def __init__(self, W, b ): # 신경망에 필요한 가중치와 바이어스를 신경망에 셋팅하는 함수
self.W = W # 클래스를 가지고 객체화(제품화) 시킬때 필요한 가중치를 self.W 에 입력
self.b = b # 클래스를 가지고 객체화(제품화) 시킬때 필요한 가중치를 self.b 에 입력
self.x = None # 순전파일때 입력값을 저장할 빈 컵을 생성합니다.
self.dW = None # 역전파할때 계산된 가중치의 기울기를 담을 변수 생성
self.db = None # 역전파할때 계산된 바이어스의 기울기를 담을 변수 생성
def forward(self, x): # 입력값과 가중치를 내적하고 바이어스를 더하는 순전파 함수 생성
self.x = x # 입력값 행렬이 self.x 에 입력됨
out = np.dot( x, self.W ) + self.b # 입력값 행렬과 가중치를 내적하고 바이어스를 더해서 out 변수에 할당
return out
def backward(self, dout):
dx = np.dot( dout, self.W.T)
self.dW = np.dot( self.x.T, dout)
self.db = np.sum( dout, axis = 0 )
return dx
문제113. 위에서 만든 Affine 계층 설계도를 가지고 객체화 시켜서 설현 사진 5장을 입렵하시오.
x = np.random.randn( 5, 32*32 ) # 설현사진 5장
W = np.random.randn(32*32, 3 ) # 뉴런 3개의 은닉층
b = np.random.randn(1, 3)
affine1 = Affine(W,b)
affine1.forward(x)
문제114. 위의 설현사진 5장에 대한 오차인 기울기 행렬을 dout을 만들고 Affine 계층의 backward 함수에 넣고 결과를 출력하시오.
x = np.random.randn( 5, 32*32 ) # 설현사진 5장
W = np.random.randn(32*32, 3 ) # 뉴런 3개의 은닉층
b = np.random.randn(1, 3) # 바이어스 생성
dout = np.random.randn(5,3) # 역전파 오차 행렬
affine1 = Affine(W,b)
affine1.forward(x)
affine1.backward(dout)
문제115. 문제114번의 실행결과 중 self.db에 있는 값을 출력하시오.
x = np.random.randn( 5, 32*32 ) # 설현사진 5장
W = np.random.randn(32*32, 3 ) # 뉴런 3개의 은닉층
b = np.random.randn(1, 3) # 바이어스 생성
dout = np.random.randn(5,3) # 역전파 오차 행렬
affine1 = Affine(W,b)
affine1.forward(x)
affine1.backward(dout)
affine1.db # array([-1.61199976, -1.19853196, 2.33188139])순전파일 때 (1,3)으로 보냈으니까 역전파일때도 (1,3)으로 와야합니다.
b = b - db
(1,3) (1,3) (1,3)
13 소프트 맥스 함수 with오차함수 계층 만들기 - p.177

입력 이미지가 Affine 계층과 relu계층을 통과하여 변환되고, 마지막 softmax계층에 의해서 10개의 확률이 출력됩니다. 숫자 0일 확률은 0.008이고 숫자 1일 확률은 0.00005이고 숫자 2일 확률이 0.991입니다.
+)소프트맥스함수와 오차함수의 계산 그래프

결론은 결국 y(예측값) - t(정답)이 역전파되어 신경망으로 흘러 같다는 것.
정답이 (0,1,0)이고 예측이 (0.01,0.09,0)이면 역전파되는 오차는 (0.01, -0.01, 0)
위의 오차가 앞층으로 전달됨. 이렇게 작은 오차가 전달되면 학습되는 정도도 작아짐.
문제116. 책 179페이지에 나오는 softmaxwithloss 함수 클래스를 생성하시오.
class SoftmaxWithLoss:
def __init__(self):
self.loss = None #오차를 담을 변수 생성
self.y = None #예측값을 담을 변수 생성
self.t = None #정답을 담을 변수 생성
def forward(self, x, t):
self.t = t # 정답데이터
self.y = softmax(x) #신경망에 흘러온 값들을 소프트 맥스 함수에 넣어 예측값(확률벡터)을 담음
self.loss = cross_entropy_error(self.y, self.t) #예측값과 정답을 크로스 엔트로피에 넣고 오차를 담음
return self.loss
def backward(self, dout = 1):
batch_size = self.t.shape[0]
dx = (self.y - self.t) / batch_size
return dx
문제117. 그동안 신경망에서 흘러왔던 아래의 입력값 x와 아래의 정답 t를 위의 softmaxwithloss클래스를 객체화 시킨 객체에 forward 함수에 넣고 오차를 출력하시오.
from common.functions import *
class SoftmaxWithLoss:
def __init__(self):
self.loss = None #오차를 담을 변수 생성
self.y = None #예측값을 담을 변수 생성
self.t = None #정답을 담을 변수 생성
def forward(self, x, t):
self.t = t # 정답데이터
self.y = softmax(x) #신경망에 흘러온 값들을 소프트 맥스 함수에 넣어 예측값(확률벡터)을 담음
self.loss = cross_entropy_error(self.y, self.t) #예측값과 정답을 크로스 엔트로피에 넣고 오차를 담음
return self.loss
def backward(self, dout = 1):
batch_size = self.t.shape[0]
dx = (self.y - self.t) / batch_size
return dx
x = np.random.randn(100,10)
t = np.random.randn(100,10)
swl = SoftmaxWithLoss()
print(swl.forward(x,t))
문제118. 무제117번에서 구현한 softmaxwithloss 계층의 backward함수를 실행해서 역전파되는 오차를 출력하시오.
x = np.random.randn(100,10)
t = np.random.randn(100,10)
swl = SoftmaxWithLoss()
print(swl.forward(x,t))
print(swl.backward())
ㅇ지금까지 만든 계산 그래프 4가지를 가지고 아래의 클래스 4개를 만든 이유는
1. 렐루함수 계층
2. 시그모이드 함수 계층
3. Affine 계층
4. softmax with loss 함수 계층
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2'] # 가중치 가져오는 코드
b1, b2 = self.params['b1'], self.params['b2'] # 바이어스 가져오는 코드
grads = {} # 기울기를 담을 딕셔너리 변수
batch_num = x.shape[0] # mnist 필기체 사진 100장(100, 28, 28)
# forward
a1 = np.dot(x, W1) + b1 # Affine1 (첫번째 어파인 계층), (100,784)◎(784,50) -> (100,50) + (1,50)브로드캐스트 = (100,50)
z1 = sigmoid(a1) # 1층의 시그모이드 함수, (100,50) -> 시그모이드 -> (100,50)
a2 = np.dot(z1, W2) + b2 # Affine2 (두번째 어파인 계층), (100,50)◎(50,10) -> (100,10)
y = softmax(a2) # softmax 함수를 통과해서 예측값 y 를 출력 (그림 5-28), (100,10) -> 소프트맥스 -> (100,10)
# 순전파: Affine1 --> sigmoid --> Affine2 ---> softmax ---> y값 출력
# 역전파: 오차함수 --> softmax --> Affine2 --> sigmoid --> Affine1
# backward
dy = (y - t) / batch_num # (예측값 - 정답) / 배치 --> 오차 (dy), 오차함수 --> softmax 부분
grads['W2'] = np.dot(z1.T, dy) # Affine2 의 가중치의 기울기를 구해서 grads 딕셔너리의 W2키 값으로 넣음
grads['b2'] = np.sum(dy, axis=0) # Affine2 의 바이어스의 기울기를 구해서 grads 딕셔너리의 b2키의 값으로 넣음
da1 = np.dot(dy, W2.T)
dz1 = sigmoid_grad(a1) * da1 # (1-y)*y*dout, 시그모이드 함수의 역전파를 구현
grads['W1'] = np.dot(x.T, dz1) # Affine1 계층의 가중치 W1에 대한 기울기 구해서 grads 딕셔너리의 W1키 값으로 넣음
grads['b1'] = np.sum(dz1, axis=0) # Affine1 의 바이어스의 기울기를 구해서 grads 딕셔너리의 b1키 값으로 넣음
return gradsgrads 딕셔너리 안에는 위의 2층 신경망을 학습 시키기 위한 가중치 W1,W2 바이어스 b1, b2에 대한 기울기가 들어있게 됨.
+)sigmoid_grade 함수 소개
def sigmoid_grad(x):
return (1.0 - sigmoid(x)) * sigmoid(x)
오차역전파로 기울기를 구하는 gradient함수를 이해함. 그러면 gradient 함수를 가지고 구현한 2층 신경망 전체 설계도를 가져와서 이 설계도로 network라는 객체를 생성해보겠음.
import sys, os
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
from common.functions import *
from common.gradient import numerical_gradient
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 가중치 초기화
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# x : 입력 데이터, t : 정답 레이블
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x : 입력 데이터, t : 정답 레이블
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
da1 = np.dot(dy, W2.T)
dz1 = sigmoid_grad(a1) * da1
grads['W1'] = np.dot(x.T, dz1)
grads['b1'] = np.sum(dz1, axis=0)
return gradsnetwork = TwoLayerNet(input_size = 784, hidden_size = 50, output_size = 10) #객체생성
network.gradient
문제119. 아래의 입력 데이터와 정답 데이터를 위에서 만든 network 객체의 gradient 함수에 넣고 결과를 출력하시오.
x = np.random.randn(100,784)
t = np.random.randn(100,10)
network.gradient(x,t)
