56 다중 회귀분석 이론
다중 선형회귀란? 단순 선형 회귀 분석의 목적이 하나의 독립변수만을 가지고 종속변수를 예측하기 위한 회귀모형을 만들기 위한 것이었다면 다중회귀분석의 목적은 여러개의 독립변수들을 가지고 종속변수를 예측하기 위한 회귀모형을 만드는 것
ex. 집값에 영향을 미치는 요소가 단순히 평수 하나만 있는게 아님.
(종속변수)집값 <------ (독립변수) 평수, 교통, 학군, 범죄율, 층수, 방의 갯수, 한강뷰,....
Q1 > 집값에 영향을 미치는 요소가 위의 여러가지 독립변수들 중에서 어떤 것인가?
Q2 > 집값을 예측하기 위한 다중 회귀식은 어떻게 되는가?

y = 집값(종속변수) , α = 기울기, b = 절편
위 식의 기울기를 알아내려면 행렬로 연산해서 알아내야 함. 그럴려면 아래 4가지 개념을 알아야함.
ㅇ다중회귀 수학식을 이해하기 위한 예제 - p264
예제1. 아래의 4가지 용어를 알아야 함
1. 전치행렬 : 행과 열을 교환함

2. 단위행렬 : 0으로 이루어진 행렬에서 대각선이 1인 행렬

3. 역행렬 : 자기 자신과 행렬곱(내적)했을 때 단위행렬이 되는 행렬

4. 의사역행렬 : 기본적으로 역행렬을 구하려면 행렬이 정방행렬이어야 하는데 직사각형 행렬도 역행렬을 구할 수 있도록 구현한 행렬
예제2. 아래의 방정식의 해를 구하시오.

예제3. A행렬과 B행렬을 만드시오


# R
A = matrix( c(1,3,2,4), nrow = 2, ncol = 2, byrow = T )
A
B = matrix( c(-1,2), nrow = 2, ncol = 1)
B예제4. 위에서 만든 A행렬과 B행렬을 가지고 x값을 출력하시오.

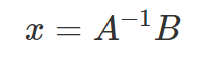
x <- solve(A) %*% B
x%*% : 행렬 곱
solve : 역행렬 구하는 함수
예제5. 위의 풀이를 파이썬으로 수행하시오.
# python
import numpy as np
A = np.array([1,3,2,4]).reshape(2,2)
B = np.array([-1,2]).reshape(2,1)
A_inv = np.linalg.inv(A) #A의 역행렬
np.dot(A_inv, B) #A의 역행렬과 B행렬의 행렬곱을 구함
문제301. 아래의 방정식의 미지수 x1, x2, x3를 출력하시오.(파이썬)
import numpy as np
A = np.array([1,4,2,0,2,1,3,5,3]).reshape(3,3)
B = np.array([1,-1,2]).reshape(3,1)
A_inv = np.linalg.inv(A)
x = np.dot(A_inv, B)
x
print('x1 = %1.0f, x2 = %1.0f, x3 = %1.0f'%(x[0,0],x[1,0],x[2,0]))
우리가 위에서 만든 A행렬은 전부 정방행렬이었음.
정반행렬은 정사각형 행렬을 뜻함.
직사각형 행렬을 아래와 같이 생성하겠음.
import numpy as np
A = np.array([1,4,2,0,2,1,3,5]).reshape(4,2)
A[[1, 4],
[2, 0],
[2, 1],
[3, 5]]
위의 직사각 행렬의 역행렬을 구하세요.
> 에러. 역행렬이 만들어지지 않음. 역행렬을 구하려면 정사각형 행렬이어야 함.
앞에서 다뤘던 데이터들(유방암, 독버섯)은 모두다 직사각형 행렬임. 이렇게 정방행렬이 아닌 직사각 행렬에 대한 역행렬을 구하려면, 자기 자신의 행렬에 자기 자신의 전치행렬을 곱하면 정방행렬이 됨. 이 정방행렬의 역행렬을 구하면 됨.
= 의사역행렬
예제6. 아래의 행렬을 R로 구현하고 아래 행렬의 전치행렬을 구하시오.
# 전치행렬 구하기
A <- matrix( c(1,2,3,4,5,6), nrow = 2, ncol = 3, byrow = T)
t(A) # 전치
예제7. 아래의 단위행렬 R로 구현하시오.
단위행렬은 대각선의 원소가 모두 1이고 나머지 원소는 모두 0인 행렬
# 단위행렬
B <- diag(3) # 3x3짜리 단위행렬
B예제8. 자기자신과 단위행렬을 행렬곱하면 자기 자신이 되는지 확인하시오.
A %*% B
예제9. 264페이지에 나오는 식의 도출과정을 먼저 이해하시오.(이때 A는 직사각 행렬)

1) 전치행렬을 곱해서 정방행렬로 만듦

2) 정방행렬의 역행렬을 곱해서 단위행렬로 만듦 = x를 구함

문제302. 위의 내용을 이해하고 아래의 방정식의 미지수 x1, x2, x3를 R로 구하시오
A <- matrix( c(1,1,2,3,4,1,3,7,1,4,2,3), nrow = 4, ncol = 3, byrow = T)
B <- matrix( c(0,6,9,3), nrow = 4, ncol = 1)
A_T <- t(A) # 전치행렬
ATA_1 <- solve(A_T %*% A) # 역행렬
x <- ATA_1 %*% A_T %*% B
x [,1]
[1,] 1
[2,] 1
[3,] -1
문제303. 아래의 방정식의 미지수 x1,x2,x3를 파이썬으로 구현하시오.
# python
import numpy as np
A = np.array([1,1,2,3,4,1,3,7,1,4,2,3]).reshape(4,3)
B = np.array([0,6,9,3]).reshape(4,1)
A_T = A.T
ATA_inv = np.linalg.inv(np.dot(A_T,A))
x = np.dot(np.dot(ATA_inv, A_T),B)
print('x1 = %1.0f, x2 = %1.0f, x3 = %1.0f'%(x[0,0],x[1,0],x[2,0]))

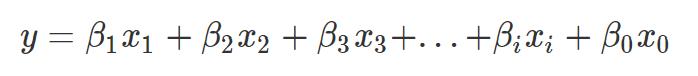
b0x0 = 절편이고 b1~bi는 기울기를 나타냄.
ㅇ p263에 나오는 다중회귀의 기울기와 절편을 구하는 R코드 구현
reg <- function(y,x){
x <- as.matrix(x) # x에 들어오는 값들을 행렬로 변환하는 코드
x <- cbind(intercept = 1,x) #intercept는 컬럼명을 붙여준 것임. 그냥 1만 써도 됨, 절편+독립변수 행렬
beta <- solve(t(x) %*% x) %*% t(x) %*% y # 기울기 구하는 수학식
colnames(beta) <- "estimate" #수치예측이라는 컬럼명 지정
print(beta)
}
cha <- read.csv("c:\\data\\challenger.csv")
head(cha)
x <- cha[,-1]
y <- cha[,1]
reg(y,x) estimate
intercept 3.527093383
temperature -0.051385940
field_check_pressure 0.001757009
flight_num 0.014292843
model <- lm(distress_ct ~ ., data = cha)Coefficients:
(Intercept) temperature field_check_pressure flight_num
3.527093 -0.051386 0.001757 0.014293
> lm()으로 구한 기울기와 다중회귀 함수 만들어서 구한 기울기의 값이 같음을 확인할 수 있음.
> y = -0.051386*x1 + 0.001757*x2 + 0.014293*x3 + 3.527093
문제304. (오늘의 마지막 문제) 스마트폰 만족도(종속변수)에 영향을 미치는 요소중 가장 영향력이 큰 독립변수는 무엇인가?
데이터 : multi_hg.csv
reg <- function(y,x){
x <- as.matrix(x) # x에 들어오는 값들을 행렬로 변환하는 코드
x <- cbind(intercept = 1,x) #intercept는 컬럼명을 붙여준 것임. 그냥 1만 써도 됨, 절편+독립변수 행렬
beta <- solve(t(x) %*% x) %*% t(x) %*% y # 기울기 구하는 수학식
colnames(beta) <- "estimate" #수치예측이라는 컬럼명 지정
print(beta)
}
smart <- read.csv("c:\\data\\multi_hg.csv", header = T)
head(smart)
x <- smart[,-4]
y <- smart[,4]
reg(y,x) estimate
intercept 3.5136006
외관 0.2694261
편의성 0.2105249
유용성 0.1623154
'Study > class note' 카테고리의 다른 글
| 머신러닝 / 다중공선성 실험하기(R 과 파이썬), 다중회귀분석 모델을 파이썬을 구현 (0) | 2022.02.15 |
|---|---|
| 머신러닝 / 다중회귀분석 모델을 R 로 구현 (0) | 2022.02.14 |
| 머신러닝 / 다중 공선성, 상관관계 분석, 단순회귀분석 모델 구현(R, 파이썬) (0) | 2022.02.11 |
| 머신러닝 / 회귀분석(수치예측) (0) | 2022.02.10 |
| 머신러닝 / 규칙기반 알고리즘(oneR, Riper) 파이썬 구현 (0) | 2022.02.10 |



