3 미니배치 - p.115
훈련 데이터중에 일부만 골라서 학습하는 방법
표본을 뽑아서 학습 시킴
ex1. 6만장을 한번에 신경망에 넣어서 학습시키는게 가능한가?
수학적으로는 가능하지만 컴퓨터로는 불가능. 컴퓨터 메모리가 초과하면서 out of memory 에러 남.
ex2. 6만장 중에 1장씩 뽑아서 학습 시키는 것은 가능한가?
학습은 되지만 시간이 너무 오래 걸림
ex3. 6만장 중에 100장씩 뽑아서 학습시킨다면?
데이터 6만장을 100장 단위로 입력. 학습을 빠르게 할 수 있음.(행렬계산에 최적화된 numpy모듈이 있기 때문)

이때 100장의 데이터는 랜덤으로 추출(복원 추출)된다. 100장씩 600번을 학습시키면 그게 바로 1epoch.
예제1. 숫자 1 ~ 60000까지의 숫자들 중에서 무작위로 10개를 추출하시오.
import numpy as np
print(np.random.choice(np.arange(1,60001),10))
예제2. 이번에는 100개를 무작위 추출하시오.
import numpy as np
print(np.random.choice(np.arange(1,60001),100))
예제3. 배치 작업을 신경망에서 수행하는 텐서 플로우 코드는 무엇인가?
model.fit(x_train, y_train,
epochs = 30,
batch_size = 100)
텐서플로우가 알아서 입력 데이터에서 100장을 랜덤 추출해서 신경망에 입력하니까 우리가 구체적인 파이썬 코드를 일일이 작성하지 않아도 되고 대신 배치 사이즈를 얼마나 주는게 좋은지만 생각하면 됩니다.
1. 배치 사이즈 클 때 : 학습 속도는 빨라지지만 학습이 잘 안될 수 있음(정확도가 좀 떨어질 수 있음)
2. 배치 사이즈 작을 때 : 학습속도가 느리지만 오래 기다리면 정확도가 좋은 결과에 수렴함.
예제4. batch_size = 100, batch_size = 5000 일때 모델의 오차와 정확도를 확인하기.
# 1. 필요한 패키지 가져오는 코드
import tensorflow as tf # 텐써 플로우 2.0
from tensorflow.keras.datasets.mnist import load_data # 텐써플로우에 내장되어있는
# mnist 데이터를 가져온다.
from tensorflow.keras.models import Sequential # 모델을 구성하기 위한 모듈
from tensorflow.keras.layers import Dense # 완전 연결계층을 구성하기 위한 모듈
from tensorflow.keras.utils import to_categorical # one encoding 하는 모듈
tf.random.set_seed(777)
(x_train, y_train), (x_test, y_test) = load_data(path='mnist.npz') # mnist 데이터 로드
# 2. 정규화 진행
# 3차원 ---> 2차원으로 차원축소하고서 정규화 진행 ( 한 픽셀이 0~255 로 되어있는데)
# 0 ~ 1 사이로 변경
x_train = (x_train.reshape((60000, 28 * 28))) / 255
x_test = (x_test.reshape((10000, 28 * 28))) / 255
# 3. 정답 데이터를 준비한다.
# 하나의 숫자를 one hot encoding 한다. (예: 4 ---> 0 0 0 0 1 0 0 0 0 0 )
y_train = to_categorical(y_train) # 훈련 데이터의 라벨(정답)을 원핫 인코딩
y_test = to_categorical(y_test) # 테스트 데이터의 라벨(정답)을 원핫 인코딩
# 4. 모델을 구성합니다. 3층 신경망으로 구성
model = Sequential()
model.add(Dense(64, activation = 'relu', input_shape = (784, ))) # 1층
model.add(Dense(32, activation = 'relu')) # 2층
model.add(Dense(10, activation = 'softmax')) # 3층 출력층
# 5. 모델을 설정합니다. ( 경사하강법, 오차함수를 정의해줍니다. )
model.compile(optimizer='adam',
loss = 'categorical_crossentropy',
metrics=['acc']) # 학습과정에서 정확도를 보려고
#6. 모델을 훈련시킵니다.
history = model.fit(x_train, y_train,
epochs = 30, # 30에폭
batch_size = 100)
# 7.모델을 평가합니다. (오차, 정확도가 출력됩니다.)
model.evaluate(x_test, y_test)
# 8.테스트 데이터의 예측값을 출력합니다.
results = model.predict(x_test)
#9. 정확도를 확인합니다.
import numpy as np
y_hat = np.argmax(results, axis=1)
y_label = np.argmax(y_test,axis=1)
print ( np.sum( y_hat == y_label ) / len(y_test) )배치 사이즈 100일때의 오차와 정확도
[0.14209480583667755, 0.9732000231742859]
#6. 모델을 훈련시킵니다.
history = model.fit(x_train, y_train,
epochs = 30, # 30에폭
batch_size = 5000)
# 7.모델을 평가합니다. (오차, 정확도가 출력됩니다.)
model.evaluate(x_test, y_test)배치사이즈 5000일때의 오차와 정확도
[0.13452723622322083, 0.9610999822616577]
4 수치미분 - p.121
"신경망을 학습 시킬때 미분이 필요"
-> 가중치를 갱신해주기 위해서 미분 필요
가중치 = 가중치 - 기울기
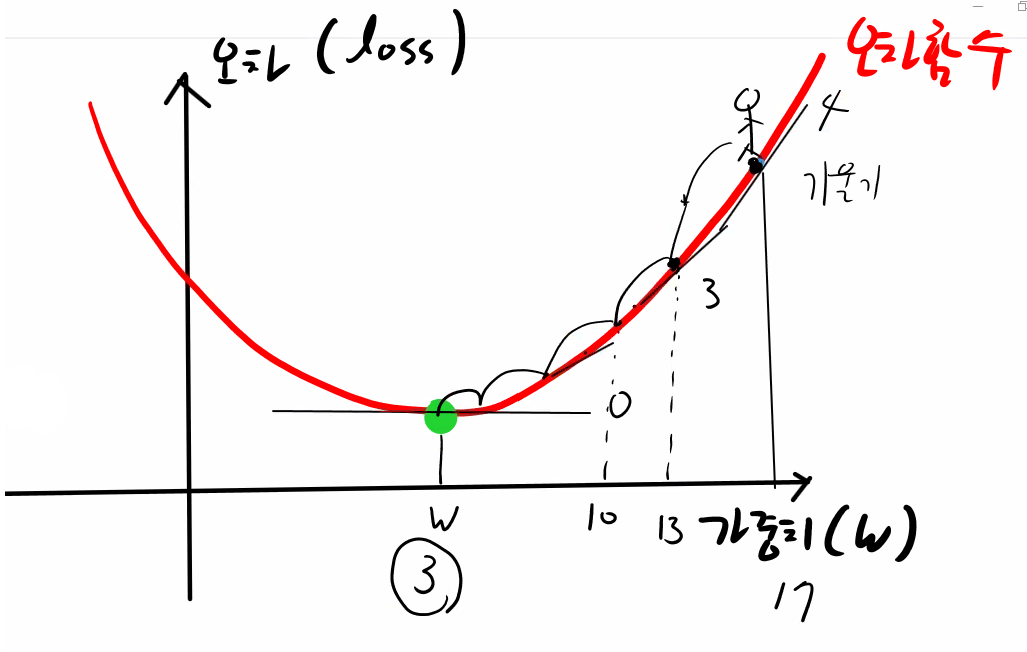
위의 그림에서 시작되는 가중치의 오차는 큰 오차. 왜냐면 처음에 생성된 가중치는 랜덤으로 생성된 값이기 때문. 오차가 가장 작은 w지점으로 가는데 목표. 그럴려면 지금 있는 곳에서 어느쪽으로 기울어졌는지 기울기를 구해야함. 기울기 구하는데 미분이 필요함.
가중치 = 가중치 - 기울기를 계속 반복학습해 기울기가 0이 될때까지 계속 학습을 함.

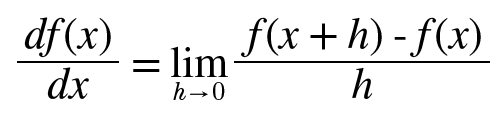
문제64. 미분 공식을 파이썬으로 구현하시오.
def numerical_diff(f,x): #미분하는 함수, 기울기 구하는 함수
h = 1e-50 #0은 아닌데 0에 가까워지는 수를 표현
return (f(x+h) - f(x))/h
문제65. 위의 오차함수를 f 라는 이름으로 생성하시오.
def f(x):
return 2*x**2 + 2
문제66. 위에서 만든 numerical_diff함수에 위의 오차함수 f를 넣고 x값에는 4를 대입해 결과를 출력하시오.
import numpy
def numerical_diff(f,x): #미분하는 함수, 기울기 구하는 함수
h = 1e-50 #0은 아닌데 0에 가까워지는 수를 표현
return (f(x+h) - f(x))/h
def f(x):
return 2*x**2 + 2
print(numerical_diff(f,4)) # 016이 출력되어야 하는데 0이 나옴. 너무 작은값을 이용하면 컴퓨터로 계산하는데 문제가 생겨 계산되지 않음.
그래서 미세한 값으로 조정하면 다시 제대로 된 결과를 얻을 수 있음( h = 1e^-4)
def numerical_diff(f,x): #미분하는 함수, 기울기 구하는 함수
h = 1e-4 #0은 아닌데 0에 가까워지는 수를 표현
return (f(x+h) - f(x))/h
def f(x):
return 2*x**2 + 2
print(numerical_diff(f,4)) # 16.0020000000074
--위의 미분 함수 개선 포인트 2가지
1. e^-50이 아니라 e^-4로 변경
2. 진정한 접선이 아니라 근사로 구한 접선으로 변경

진정한 미분은 컴퓨터로 구현할 수 없으니 근사로 구한 접선(파란색 접선)으로 구현해야하는데 그 식은 다음과 같음.

위의 공식을 파이썬 함수로 생성하면 다음과 같음.
import numpy
def numerical_diff(f,x):
h = 1e-4 #0은 아닌데 0에 가까워지는 수를 표현
return (f(x+h) - f(x-h))/(2*h)
def f(x):
return 2*x**2 + 2
print(numerical_diff(f,4)) # 15.99999999999823816으로 값이 딱 떨어지지 않은 이유는 진정한 미분의 공식이 아니라 근사로 구한 접선의 미분이기 때문.
문제67. 아래의 오차함수를 위에서 만든 수치미분함수에 넣고 x값 6에서의 미분계수(기울기)를 출력하시오.
def numerical_diff(f,x): #수치미분함수
h = 1e-4 #0은 아닌데 0에 가까워지는 수를 표현
return (f(x+h) - f(x))/h
def f(x):
return 3*x**2 + 2*x + 7
print(numerical_diff(f,6)) # 38.00030000007837
4 편미분 - p.125
미분은 오차함수의 기울기를 구해서 가장 오차가 작은 지점(global minimum)을 찾기 위해 가중치를 갱신하기 위해서 필요하다는 것을 알았는데, 그렇다면 왜 편미분이 필요한가?
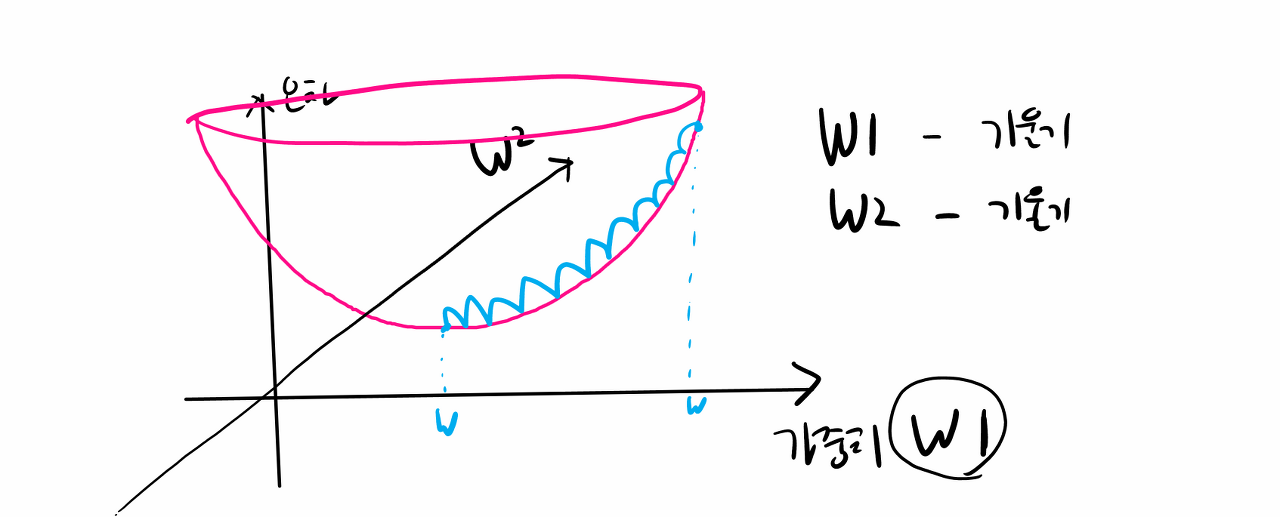


편미분이랑 변수가 2개 이상인 함수를 미분할 때 미분 대상 변수외에 나머지 변수를 상수처럼 고정시켜 미분하는 것을 편미분이라고 함.

w1 = w1 - 기울기 ----> 기울기가 0이 될 때까지 계속 w1을 갱신
w2 = w2 - 기울기 ----> 기울기가 0이 될 때까지 계속 w2을 갱신
오차함수(f)에 대해서 w1에 대해서만 미분한다면 그냥 미분 함수를 이용하면 되는데 w1도 미분하고 w2도 미분하고 w3도 오차함수를 미분해야하므로 "편미분"을 사용합니다.
문제68. 아래의 함수를 편미분해서 x,y 좌표가 (3,2)지점의 기울기를 구하시오.

문제69. 오차함수를 파이썬으로 생성하시오.
import numpy as np
def loss_func(x):
return x[0]**2 + x[1]**2
x = np.array([3.0,4.0])
print(loss_func(x)) #25
문제70. 위의 loss_func() 함수를 x0 = 3, x1 = 4 지점에서 x0에 대해서 편비누했을때의 기울기를 구하시오.

def function_tmp1(x0):
return x0**2 + 4**2 #x1은 상수 취급이 되어서 이렇게 생성됩니다.
def numerical_diff(f,x):
h = 1e-4
return ( f(x+h) - f(x-h) ) / (2*h)
x = np.array([3.0,2.0])
print(numerical_diff(function_tmp1,3)) #6.000000000003786.00000000000378에서 맨 뒤에 나온 378은 중앙차분오차 때문입니다. 근사로 구현 접선의 미분식으로 구현했기때문에 오차가 발생할 수밖에 없는데 위의 오차는 무시해도 될만한 오차입니다.
문제71. 위의 loss_func()함수를 x0=3, x1=4 지점에서 x1에 대해서 편미분했을때의 기울기는?
def function_tmp2(x1):
return 3**2 + x1**2 #x0은 상수 취급이 되어서 이렇게 생성됩니다.
def numerical_diff(f,x):
h = 1e-4
return ( f(x+h) - f(x-h) ) / (2*h)
x = np.array([3.0,2.0])
print(numerical_diff(function_tmp2,4)) #7.999999999999119중앙차분오차에 의해 8이 안나오고 7.999999999999119이 출력됨.
방금 위에서는 일일이 손으로 한쪽을 상수화해서 편미분을 함.
그런데 그냥 다 자동으로 편미분되게 코드를 짜보자.
문제72. common폴더에 gradient.py안에 편미분 함수를 가져오시오.
def numerical_gradient(f, x):
h = 1e-4 # 0.0001, 0에 가까워지는 극한값을 표현함
grad = np.zeros_like(x) # x와 형상이 같은 배열을 생성하는데 원소가 다 0으로 구성됨
#기울기 담는 변수 [0,0]
for idx in range(x.size): # 변수x의 전체 원소의 길이(len은 첫번째 차원원소길이만 출력함)
tmp_val = x[idx] #x[0] = 3.0이라고 가정
x[idx] = float(tmp_val) + h #x[0] = 3.0001로 갱신
fxh1 = f(x) # f(x+h) = f(x)함수가 갱신된 x값으로 계산됨
x[idx] = tmp_val - h # x[0] = 2.9999로 갱신
fxh2 = f(x) # f(x-h) = f(x)함수가 갱신된 x값으로 계산됨
grad[idx] = (fxh1 - fxh2) / (2*h) #미분함수
x[idx] = tmp_val # 값 복원
return grad
x = [3,4] 넣어서 편미분 해보기
def loss_func(x):
return x[0]**2 + x[1]**2
def numerical_gradient(f, x):
h = 1e-4 # 0.0001, 0에 가까워지는 극한값을 표현함
grad = np.zeros_like(x) # x와 형상이 같은 배열을 생성하는데 원소가 다 0으로 구성됨
#기울기 담는 변수 [0,0]
for idx in range(x.size): # 변수x의 전체 원소의 길이(len은 첫번째 차원원소길이만 출력함)
tmp_val = x[idx] #x[0] = 3.0이라고 가정
x[idx] = float(tmp_val) + h #x[0] = 3.0001로 갱신
fxh1 = f(x) # f(x+h) = f(x)함수가 갱신된 x값으로 계산됨
x[idx] = tmp_val - h # x[0] = 2.9999로 갱신
fxh2 = f(x) # f(x-h) = f(x)함수가 갱신된 x값으로 계산됨
grad[idx] = (fxh1 - fxh2) / (2*h) #미분함수
x[idx] = tmp_val # 값 복원
return grad
x = np.array([3.0,4.0])
print(numerical_gradient(loss_func,x)) # [6. 8.] 보이기만 정수고 실제는 소수점 다 살아있음
6 신경망에서의 기울기 - p.133
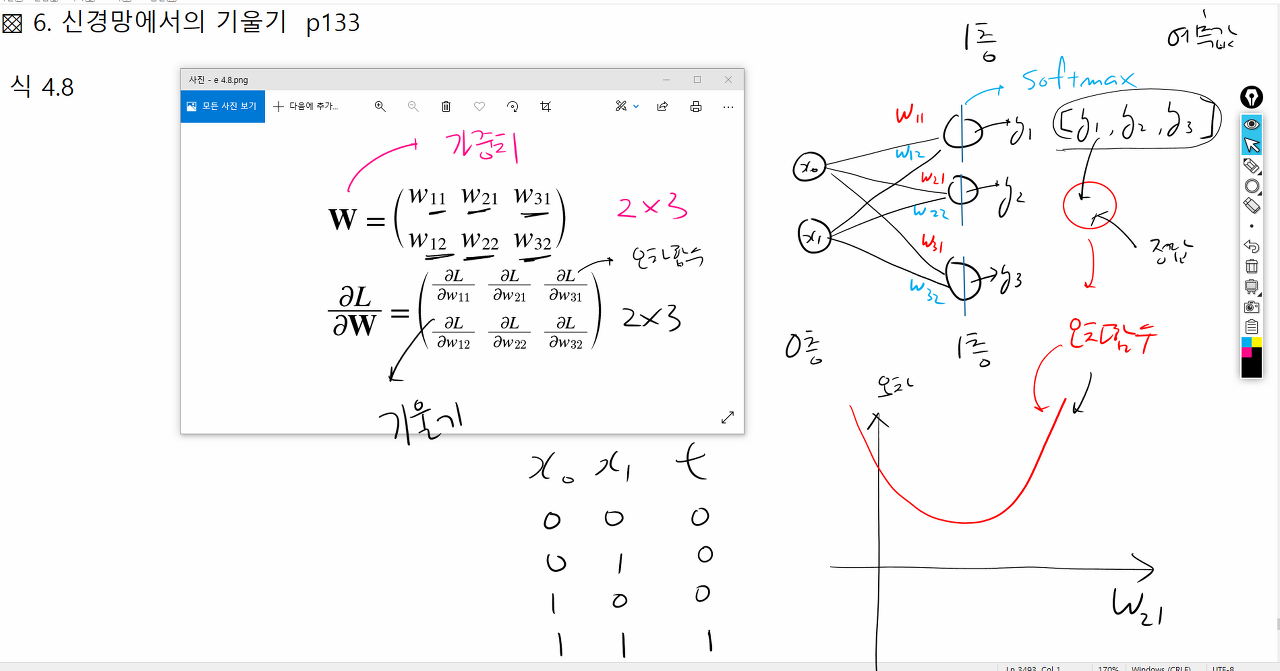
문제73. 가중치 행렬을 구성할 수 있도록 텐서플로우로 아래의 단층 신경망을 구현하시오.
#1. 필요한 패키지를 불러옵니다
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
import numpy as np
tf.random.set_seed(777)
#2. 모델 구성
model = Sequential()
model.add(Flatten(input_shape=(2,))) #입력층(0층)
model.add(Dense(3,activation = 'softmax')) #출력층(1층)
#3. 입력 데이터 만들기
x = np.array([0.6,0.9]).reshape(1,2)
#4. 정답 데이터 만들기
t = np.array([0,0,1]).reshape(1,3)
#5. 모델 설정
model.compile(optimizer = 'adam', #경사하강법
loss = 'categorical_crossentropy', #오차함수
metrics = ['acc'])
#6. 모델 훈련
model.fit(x,t,epochs = 10)
#7. 모델 평가
model.evaluate(x,t) #[0.4226197898387909, 1.0]
#8. 가중치 행렬 출력
model.get_weights()
'Study > class note' 카테고리의 다른 글
| 딥러닝 / 경사하강법, 러닝 레이트 (0) | 2022.04.07 |
|---|---|
| 딥러닝 / 텐서플로우로 신경망 구현하기 (0) | 2022.04.07 |
| 딥러닝 / 크로스엔트로피 오차함수, 평균 제곱 오차함수 (0) | 2022.04.05 |
| 딥러닝 / 배치처리 (0) | 2022.04.05 |
| 딥러닝 / 손글씨 필기체 인식하는 신경망 만들기 (0) | 2022.04.04 |



