10 파이썬 날코딩으로 2층 신경망 클래스 구현하기 - p.137
1. 텐서플로우를 이용했을 때 -> 구현이 쉽고 빠름
2. 텐서플로우를 이용하지 않았을 때 -> 신경망을 만드는게 어렵지만 원리를 이해하는데 좋음

아래와 같이 신경망 설계도를 클래스로 생성하는 이유는?
-> 객체로 찍어내기 편해서
#1. 필요한 패키지를 불러옵니다
import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.functions import softmax, cross_entropy_error #필요한 패키지(common)를 홈디렉토리에 미리 가져다 놔야함
#2. 단층신경망 클래스 생성
class simpleNet:
def __init__(self):
self.W = np.random.randn(2,3) # 정규분포로 2x3 행렬의 가중치 생성(랜덤 초기화) - 임의의 가중치
def predict( self, x ): #예측함수 : 입력값을 받아 가중치 행렬과 내적
return np.dot( x, self.W )
def loss( self, x, t ): #오차함수
z = self.predict(x) #입력값,가중치 내적결과를 z에 넣고
y = softmax(z) #z를 받아서 softmax함수에 넣고 확률벡터를 y에 넣고
loss = cross_entropy_error(y, t) #크로스 엔트로피 오차함수에 예측값 y와 정답 t를 넣고 loss출력
return loss
net = simpleNet()
print(f'가중치 행렬 : {net.W}') # 가중치 행렬 확인
# 입력값 생성
x = np.array( [0.6, 0.9] )
# 예측값
y = net.predict(x)
print(f'예측값 :{y}')
# 최대값 원소의 인덱스 확인
print (f'예측값 인덱스 : { np.argmax(y)}' )
# 오차확인
t = np.array([ 0, 0, 1]) #one hot encoding 형태로 정답 생성
print(f'label 인덱스 : {np.argmax(t)}')
print (f'오차 : { net.loss(x,t)}' )
ㅇ개와 고양이를 분류하는 신경망의 원리

개와 고양이를 분류하는 위의 3층 신경망에서 x1에 들어오는 픽셀은 고양이의 귀이고 x2에 들어오는 픽셀은 고양이의 수염. 그런데 이 고양이의 귀와 수염이 고양이와 개를 분류하는데 있어서 정말 중요한 신호라고 한다면 그 입력신호에 따른 가중치값이 학습되면서 점점 조정될 것.
고양이 얼굴이 없는 벽쪽의 픽셀들은 중요도가 낮은 신호로 처리될 것이고 고양이 사진에서 고양이의 특징을 설명하는 픽셀은 점점 신호가 커질 것. 그래서 점점 오차가 줄어들 수 있도록 가중치가 갱신될 것.
ㅇ1층 신경망을 텐서 플로우 없이 구현한 코드

ㅇ러닝 레이트(학습률)가 너무 작을 때와 너무 클 때의 차이 실험

ㅇ2층 신경망을 텐서 플로우 없이 구현하기
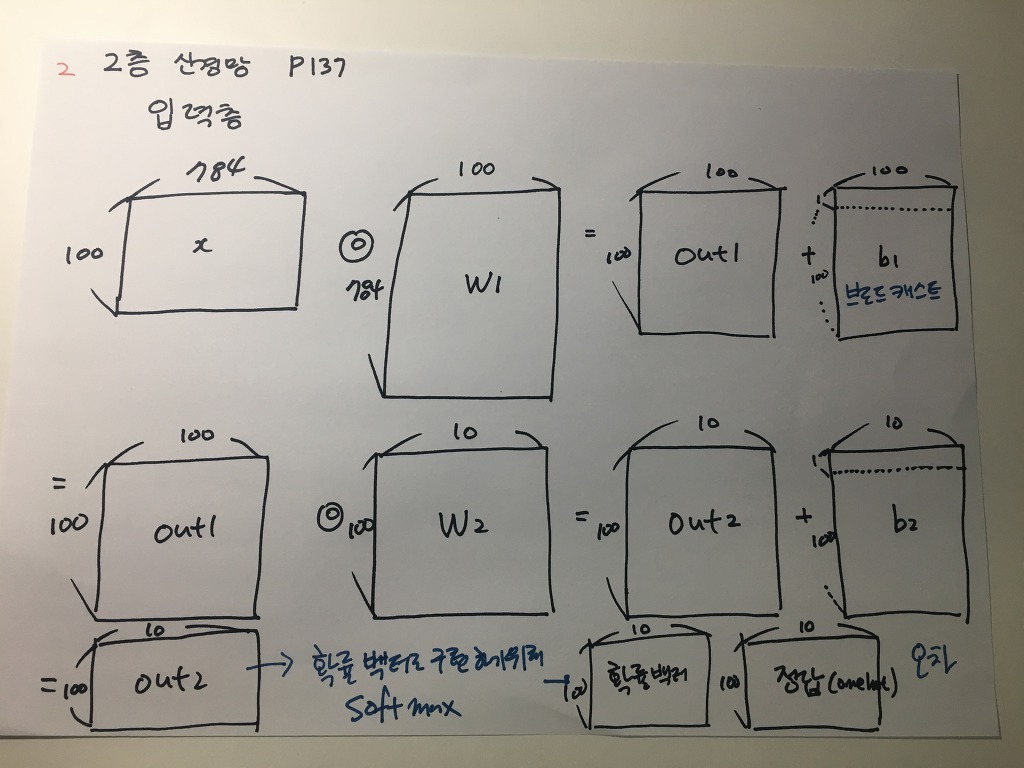
오차역전파를 이용한 코드
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
from common.functions import *
from common.gradient import numerical_gradient # 만들었던 편미분 함수 임포트(common 패키지 안에)
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 가중치 초기화
self.params = {} #가중치와 바이어스를 관리할 딕셔너리 자료구조 생성
# 학습률 ↓
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size) #(784,100)
self.params['b1'] = np.zeros(hidden_size) #(1,100) 나중에 브로드 캐스트 됨
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) #(100,10)행렬의 0으로 채워진 행렬
self.params['b2'] = np.zeros(output_size)
# 2층 신경망이 생성될 때 만들어지는 가중치와 바이어스 초기값이 params 딕셔너리에 만들어짐
# 입력값 행렬과 가중치 행렬을 내적하고 바이어스 행렬을 더해서 결과적으로 확률벡터를 출력하는 함수
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y # 확률벡터가 100가 출력(batch size = 100), 결국 (100,10)으로 출력됨
# x : 입력 데이터, t : 정답 레이블
def loss(self, x, t): #(100,784)의 입력 데이터가 들어와서
y = self.predict(x) #(100,10)의 확률 벡터가 출력
return cross_entropy_error(y, t) #(100,10)의 확률벡터와 (100,10)의 정답행렬이 오차함수로 들어감
#100개 입력값에 대한 오차 평균 1개 출력됨
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x : 입력 데이터, t : 정답 레이블
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t): #5장에서 배울 오차 역전파 함수, 텐서플로우도 오차역전파 함수로 구현됨
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
da1 = np.dot(dy, W2.T)
dz1 = sigmoid_grad(a1) * da1
grads['W1'] = np.dot(x.T, dz1)
grads['b1'] = np.sum(dz1, axis=0)
return grads
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=100, output_size=10)
# 하이퍼파라미터
iters_num = 10000 # 반복 횟수를 적절히 설정한다.
train_size = x_train.shape[0]
batch_size = 100 # 미니배치 크기
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
# 1에폭당 반복 수
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
# 미니배치 획득
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
#grad = network.numerical_gradient(x_batch, t_batch) #수치미분을 이용한 기울기
grad = network.gradient(x_batch, t_batch) #오차역전파를 이용한 기울기
# 매개변수 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 학습 경과 기록
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 1에폭당 정확도 계산
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
loss 함수 이후의 나머지 코드는 5장 끝에서 설명
반응형
'Study > class note' 카테고리의 다른 글
| 딥러닝 / 오차역전파를 이용한 2층 신경망 구현 (0) | 2022.04.11 |
|---|---|
| 딥러닝 / 패션 mnist 신경망에 사진을 넣고 잘 예측하는지 확인하기(+구글 코랩) (0) | 2022.04.10 |
| 딥러닝 / 경사하강법, 러닝 레이트 (0) | 2022.04.07 |
| 딥러닝 / 텐서플로우로 신경망 구현하기 (0) | 2022.04.07 |
| 딥러닝 / 미니배치, 수치미분, 편미분, 신경망에서 기울기 (0) | 2022.04.06 |



