ㅇ회귀트리
수치 반응변수의 예측
선형 회귀 기법을 사용하지 않음
x를 고려하지 않고 y를 예측 > 표본평균 이용 > "x가 주어졌을 때의 y의 조건부 기댓값을 추정"
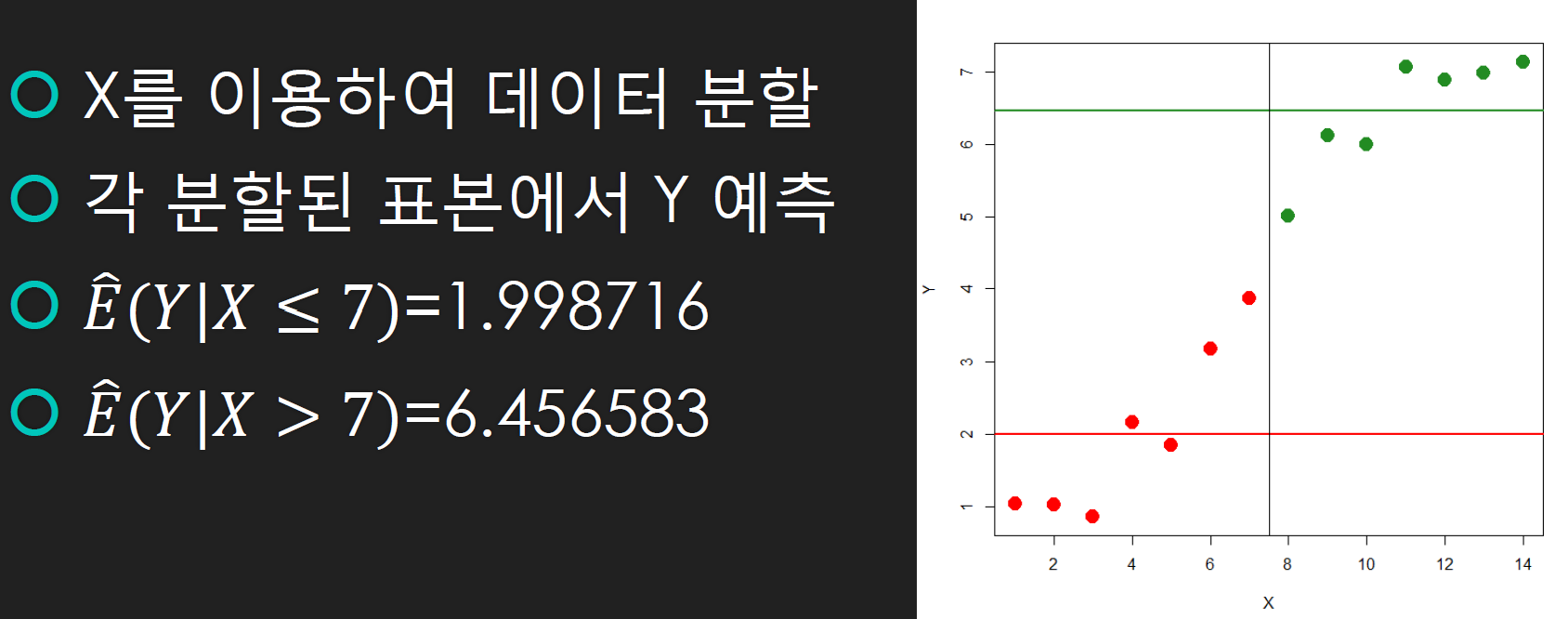

= x에 따른 y의 표본평균을 이용해 기댓값으로 분류함.
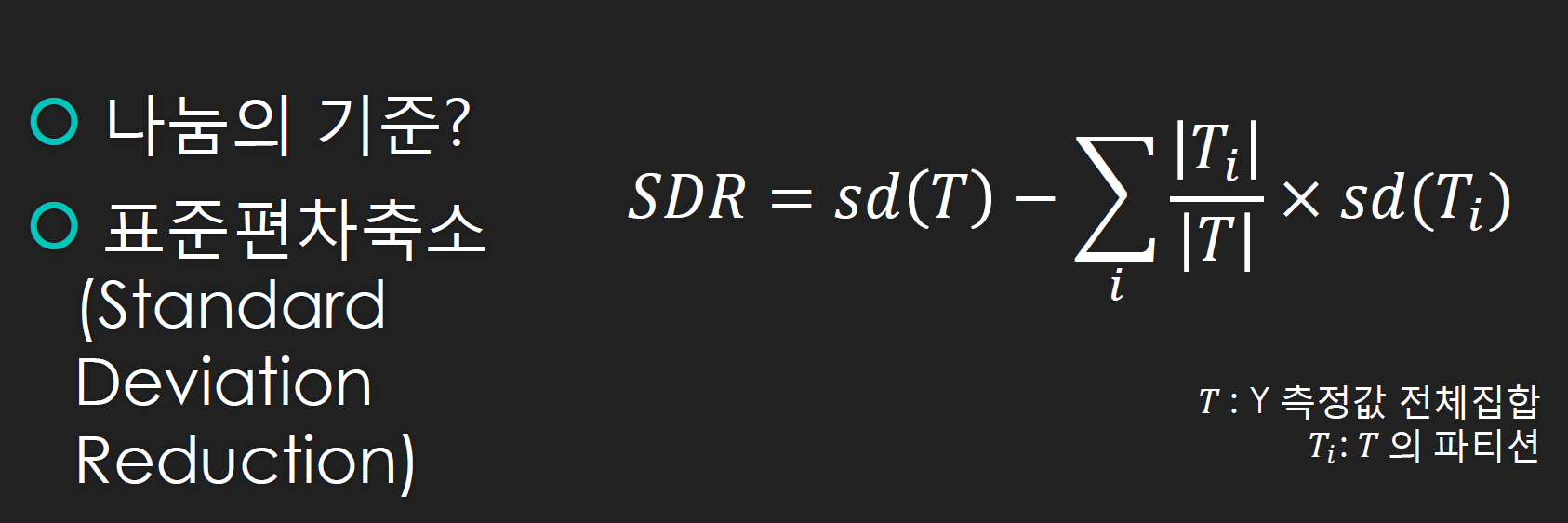

> 의사결정트리에서는 정보획득량을 기준으로 했는데, 회귀트리는 표준편차축소를 기준으로 함.
> 표준편차축소값이 가장 큰 것을 먼저 기준으로 삼음.
>독립변수가 모두 명목형, 범주형일때 종속변수가 수치일때 회귀트리를 사용함.
ㅇ p.292페이지에 나온 내용을 파이썬으로 구현하기
의사결정트리의 경우에는 정보획득량으로 가장 중요한 독립변수를 선택했는데 회귀트리의 경우 표준편차축소값으로 가장 중요한 독립변수를 선택함.
파이썬으로 회귀트리의 가장 중요한 독립변수를 선택하는 것을 실습해보겠음.

#1. 원본데이터 생성
#2. 원본데이터를 A속성으로 나누었을 때 데이터
#3. 원본데이터를 B속성으로 나누었을 때 데이터
#4. A속성으로 나누었을 때의 SDR
#5. B속성으로 나누었을 때의 SDR
#6. 두 속성 중 SDR이 큰 것으로 데이터를 속성에 따라 평균값을 각각 구함
#1. 원본데이터 생성
tee = [1,1,1,2,2,3,4,5,5,6,6,7,7,7,7]
#2. 원본데이터를 A속성으로 나누었을 때 데이터
at1 = [1,1,1,2,2,3,4,5,5]
at2 = [6,6,7,7,7,7]
#3. 원본데이터를 B속성으로 나누었을 때 데이터
bt1 = [1,1,1,2,2,3,4]
bt2 = [5,5,6,6,7,7,7,7]
#4. A속성으로 나누었을 때의 SDR
import numpy as np
np.std(tee, ddof = 1) #ddof 자유도ddof는 자유도. 이 값은 np.std에서 기본값이 0임. 표본으로 보고 자유도를 1로 계산해야 R과 동일한 결과가 출력됨.
#4. A속성으로 나누었을 때의 SDR
import numpy as np
sdr_a = np.std(tee,ddof=1) - (len(at1)/len(tee) * np.std(at1,ddof=1) + len(at2)/len(tee) * np.std(at2, ddof=1))
sdr_a #1.2028145680979165
#5. B속성으로 나누었을 때의 SDR
sdr_b = np.std(tee,ddof=1) - (len(bt1)/len(tee) * np.std(bt1,ddof=1) + len(bt2)/len(tee) * np.std(bt2, ddof=1))
sdr_b #1.3927513935303917
#6. 두 속성 중 SDR이 큰 것으로 데이터를 속성에 따라 평균값을 각각 구함
np.mean(bt1) #2.0
np.mean(bt2) #6.25sdr값이 큰 B속성으로 데이터를 나눴을 때, bt1에 속하면 결과값이 2.0으로 예측되고, bt2에 속하면 결과값이 6.25로 예측됨.
ㅇ다음의 데이터 프레임을 만들고 아래의 3개의 속성 중 pattern, outline, dot중에 어느 속성으로 area를 나누는게 더 좋은지 실험하기
#1. 데이터프레임 생성
import pandas as pd
a = {'pattern' : [ '수직', '수직', '대각선', '수평', '수평', '수평', '수직', '수직', '대각선', '수평', '수직', '대각선', '대각선', '수평' ],
'outline' :[ '점선', '점선', '점선', '점선', '실선', '실선', '실선', '점선', '실선', '실선', '실선', '점선', '실선', '점선' ],
'dot' : [ '무', '유', '무', '무', '무', '유', '무' , '무', '유', '무', '유', '유', '무', '무' ],
'area' :[25, 30, 46, 45, 52, 23, 43, 35, 38, 46, 48, 52, 44, 30 ] }
df = pd.DataFrame(a)
list_df = list(df.area)
list_df
#2. pattern으로 area를 분류했을 때 SDR
pt1 = list(df.loc[df.pattern == '수직','area'])
pt2 = list(df.area[df.pattern == '수평'])
pt3 = list(df.area[df.pattern == '대각선'])
sdr_pt = np.std(list_df, ddof = 1) - ( len(pt1)/len(list_df) * np.std(pt1, ddof=1) +
len(pt2)/len(list_df) * np.std(pt2, ddof=1) +
len(pt3)/len(list_df) * np.std(pt3, ddof=1) )
sdr_pt #0.338370410662689
#3. outline으로 area를 분류했을 때 SDR
out1 = list(df.area[df.outline == '점선'])
out2 = list(df.area[df.outline == '실선'])
sdr_out = np.std(list_df, ddof = 1) - ( len(out1)/len(list_df) * np.std(out1, ddof=1) +
len(out2)/len(list_df) * np.std(out2, ddof=1) )
sdr_out #-0.10086200041392779
#4. dot로 area를 분류했을 때 SDR
dot1 = list(df.area[df['dot'] == '유'])
dot2 = list(df.area[df['dot'] == '무'])
sdr_dot = np.std(list_df, ddof = 1) - ( len(dot1)/len(list_df) * np.std(dot1, ddof=1) +
len(dot2)/len(list_df) * np.std(dot2, ddof=1) )
sdr_dot #-0.2680833272047334> SDR이 가장 높은 독립변수가 pattern. 그래서 pattern하나로 area를 분류한다면 다음과 같이 분류한 값을 가지고 각각 평균값을 구하면 됨.
print(np.mean(pt1)) #36.2
print(np.mean(pt2)) #39.2
print(np.mean(pt3)) #45.0
61 R 로 회귀트리 구현하기 - p.294
와인의 품질(수치형)을 예측하는 회귀트리 모델을 생성
#1. 데이터 로드
#2. 종속변수 정규분포 확인
#3. 결측치 확인
#4. 훈련데이터와 테스트데이터 분리(9:1)
#5. 훈련데이터로 모델 생성
#6. 모델 시각화
#7. 훈련된 모델로 테스트 데이터 예측
#8. 모델 성능 평가
#9. 모델 성능 개선
# R
#1. 데이터 로드
wine <- read.csv("c:\\data\\whitewines.csv")
head(wine)
colnames(wine) # 컬럼확인"fixed.acidity" : 고정산도
"volatile.acidity" : 휘발성 산도
"citric.acid" : 시트르산
"residual.sugar" : 잔류 설탕
"chlorides" : 염화물
"free.sulfur.dioxide" : 자유 이산화황
"total.sulfur.dioxide" : 총 이산화황
"density" : 밀도
"pH" : pH
"sulphates" : 황산염
"alcohol" : 알코올
"quality" : 품질(label)
#2. 종속변수 정규분포 확인
hist(wine$quality)
> 정규성을 보이고 있음 - 결과가 잘 예측될거라고 예상됨
#3. 결측치 확인
colSums(is.na(wine)) #결측치 없음
#4. 훈련데이터와 테스트데이터 분리(9:1)
library(caret)
set.seed(1)
train_num <- createDataPartition(wine$quality, p = 0.9, list = F)
train_data <- wine[train_num, ]
test_data <- wine[-train_num, ]
nrow(train_data) #4409
nrow(test_data) #489
#5. 훈련데이터로 모델 생성
install.packages("rpart")
library(rpart)
model <- rpart(quality ~., data = train_data)
model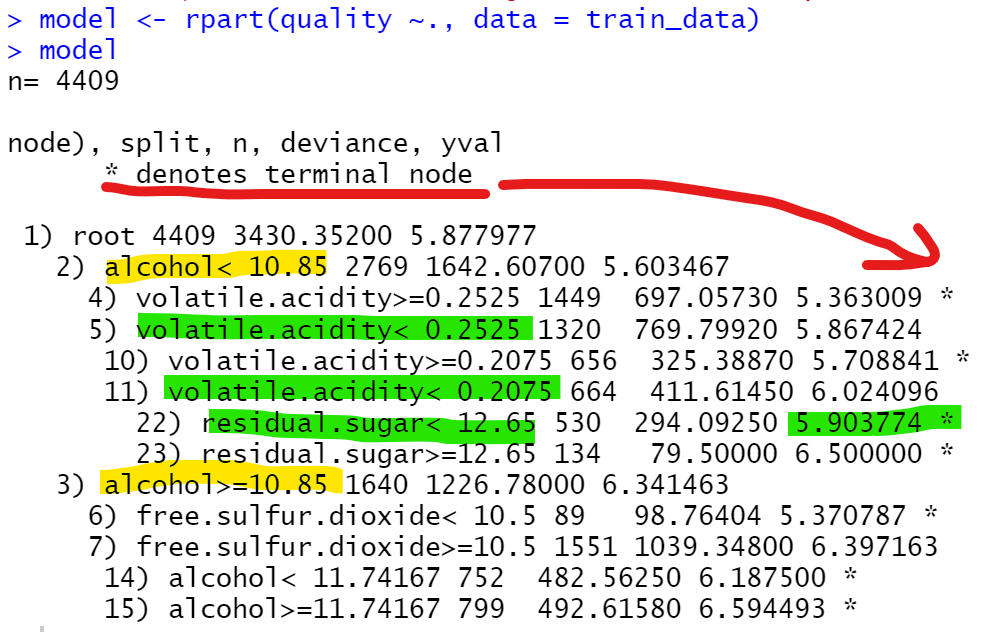
> *표시가 있는 노드는 잎노드로 노드에서 예측이 이루어진다는 것
> wine의 quality는 3~9등급으로 구성되어져 있는데,
예를 들어 alcohol <10.85이고 volatile.acidity < 0.2525면서 volatile.acidity < 0.2075 이고 residual.sugar < 12.65 인 것은 quality를 5.9로 예측함.
#6. 모델 시각화
install.packages("rpart.plot")
library(rpart.plot)
rpart.plot(model, digit = 3) #digit = 3은 소수점 세번째에서 반올림

#7. 훈련된 모델로 테스트 데이터 예측
result <- predict(model, test_data[, -12])
result # 결과가 실수형으로 출력됨
#8. 모델 성능 평가
cor(result, test_data[, 12]) #0.5150889> 회귀분석할 때는 성능을 결정계수로 확인했음. 그런데 회귀트리의 경우는 결정계수가 없음. 다른 방법으로 성능을 평가해야함. 분류의 경우는 정확도로 확인을 했는데 지금 이 경우는 분류가 아닌 수치예측임.
실제 정답과 지금 예측한 값이 똑같지는 않음. 따라서 이 경우에는 얼마나 상관관계가 있는가로 평가해야함.
#9. 예측값과 실제값의 오차 확인>성능 평가
mae <- function(actual, predicted){mean(abs(actual - predicted))} # abs는 절대값
mae(test_data[,12], result) #0.640367> 상관계수는 1에 가까워야하고 오차는 0에 가까워야 함.
#10. 모델 성능 개선
회귀트리 자체에서 개선시킬 수는 없음. 회귀트리를 모델트리로 바꿔줘서 성능 개선 시킴.
문제322. (점심시간 문제) 위에서 시각화한 회귀트리 모델을 다시 시각화하는데 책 p302 처럼 옵션을 사용해서 시각화 하시오.
rpart.plot(model, digits = 4, fallen.leaves = TRUE, type = 3, extra = 101,
box.palette = "BuRd",clip.right.labs = FALSE,
split.cex = 1.2)
https://cran.r-project.org/web/packages/rpart.plot/rpart.plot.pdf
fallen.leaves = TRUE : box를 바닥에 붙이느냐 안 붙이느냐
type = 3
extra = 101 리프 box 크기 스타일
box.palette = "BuRd" : box 색깔 지정
clip.right.labs = FALSE : 오른쪽에도 label표시하기
split.cex = 1.2 : 질문 텍스트 크기 지정
62 모델트리 이론
모델트리는 잎 노드를 회귀모델로 대체함으로써 회귀트리를 확장하는 개념

63 R 로 모델트리 구현하기
회귀트리는 무조건 분할한 y(종속변수의 값들) 값들의 평균값으로만 예측을 했는데 모델트리는 분할한 x값과 y값들에 대한 회귀식을 통해서 y값을 예측함. 그래서 회귀트리보다 모델트리가 오차가 더 작음.
#10. 모델 성능 개선
install.packages("Cubist")
library(Cubist) # 모델트리 패키지 라이브러리
model2 <- cubist(x = train_data[,-12], y = train_data[,12]) # 모델생성
result2 <- predict(model2, test_data[,-12]) # 모델예측
cor(result2, test_data[,12]) #0.51 -> 0.5954519로 증가함
mae(test_data[,12], result2) #0.64 -> 0.5738158로 오차가 줄어듦> 회귀트리에서 모델트리로 변경했을 때 상관계수는 늘어났고 오차는 줄어들었음. 아주 극적으로 개선되지는 않았지만 성능개선 효과가 있었음. 조금 더 성능을 올리고 싶다면 뒤에 11장에서 배울 앙상블을 이용하여 수치예측을 하면 되는데 앙상블을 이용하여 수치예측하는 알고리즘 중에 랜덤포레스트 회귀가 있음.
'Study > class note' 카테고리의 다른 글
| 머신러닝 / 신경망 이론 (0) | 2022.02.16 |
|---|---|
| 머신러닝 / 파이썬으로 회귀트리 구현하기 (0) | 2022.02.16 |
| 머신러닝 / 회귀트리 (0) | 2022.02.15 |
| 머신러닝 / 다중공선성 실험하기(R 과 파이썬), 다중회귀분석 모델을 파이썬을 구현 (0) | 2022.02.15 |
| 머신러닝 / 다중회귀분석 모델을 R 로 구현 (0) | 2022.02.14 |


