6장
1. 언더 피팅을 방지하는 방법
- 가중치 초기값 설정
- 경사하강법의 종류
- 배치 정규화
2. 오버 피팅을 방지하는 방법
- 드롭아웃
- L2 정규화(가중치 감소)
1 가중치 초기값 - p202
신경망 초기 셋팅시 랜덤으로 생성되는 가중치 W와 바이어스 b의 초기갓을 어떻게 선정하느냐에 따라서 학습이 잘 될수도 있고 잘 안될수도 있음.

학습이 잘 되려면 가중치 초기값들의 분포가 정규분포 형태를 이루어야 함.
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 가중치 초기화
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)결국 다음과 같이 만든 것
W1 = np.random.randn(784, 100)
W1
numpy의 random의 randn으로 난수를 생성하게 되면 가우시안 정규분포를 따르는 난수들이 생성됨
생성되는 가중치의 표준편차가 너무 큰 경우와 너무 작은 경우는 어떤 경우인가?
1. 생성되는 가중치의 표준편차가 너무 큰 경우
ex. 시험문제가 너무 어려우면 아주 잘하는 학생들과 아주 못하는 학생들로 점수가 나뉨
W1 = 100 * np.random.randn(784,100)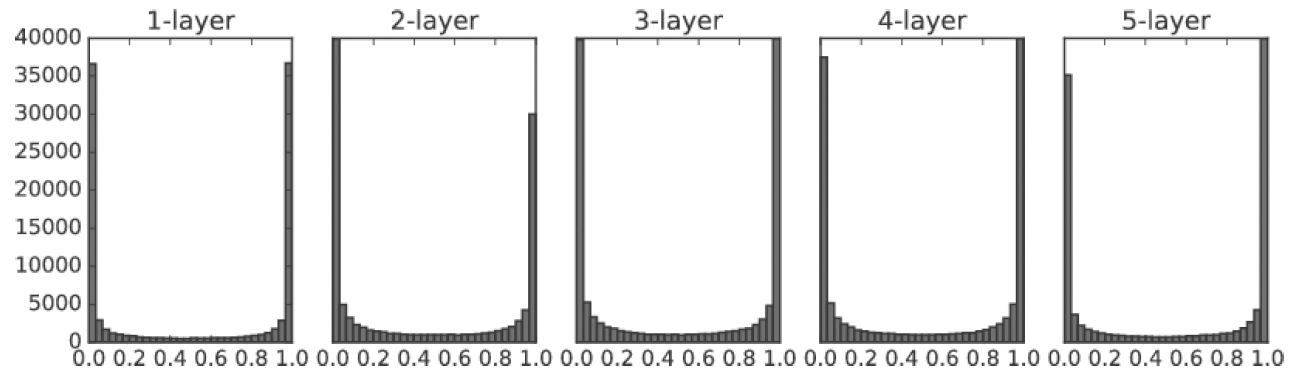
2. 생성되는 가중치의 표준편차가 너무 작은 경우
ex. 시험문제가 너무 쉬우면 학생들의 점수가 평균에 가까워짐.
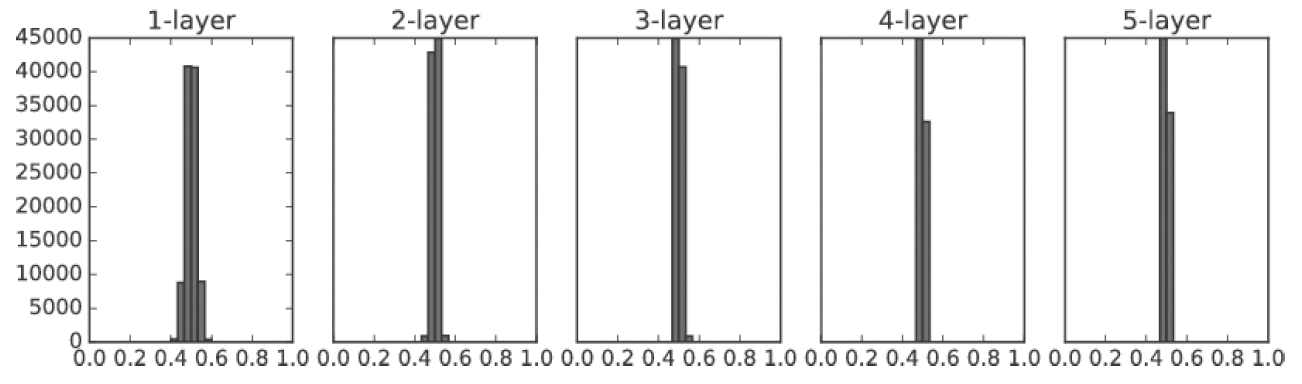
W1 = 0.00001 * np.random.randn(784,100)
문제137. 오전에 만들었던 파이썬 날코딩 2층 신경망에 가중치 초기값을 다음과 같이 변경하고 실험하시오.
net = TwoLayerNet(weight__init_std = 0.0001)
import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.functions import softmax, cross_entropy_error, sigmoid , sigmoid_grad
# common 폴더 안에 functions.py 모듈안에 softmax 함수와 cross_entropy_error 함수를 가져와라
from tensorflow.keras.utils import to_categorical
from common.gradient import numerical_gradient
class TwoLayerNet:
def __init__(self, weight__init_std): # multipleNet 클래스(설계도)의 객체(제품)가 만들어질 때 자동으로 실행되는 함수
self.params={}
self.params['W1'] = weight__init_std * np.random.randn(784,50) # 1층의 가중치
self.params['b1'] = weight__init_std * np.zeros(50) # 1층의 바이어스
self.params['W2'] = weight__init_std * np.random.randn(50,10) # 2층(출력층)의 가중치
self.params['b2'] = weight__init_std * np.zeros(10) # 2층(출력층)의 바이어스
print('2층 신경망이 생성되었습니다')
def predict( self, x ):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
k = np.dot( x, W1 ) + b1 # 1층
k_prime = sigmoid(k) # 1층 시그모이드
m = np.dot( k_prime, W2) + b2 # 2층(출력층)
n = softmax(m) # 2층(출력층) 의 소프트 맥스 함수
return n
def loss( self, x, t ):
z = self.predict(x) # 입력값을 받아서 은닉 3층에서 발생한 값을 z변수에 입력
loss = cross_entropy_error(z, t) # 확률벡터와 원핫인코딩된 정답을 받아서 오차를 출력하는 함수
return loss
def accuracy(self,x, t):
y = self.predict(x)
y = np.argmax(y, axis=1) # 예측한 숫자
t = np.argmax(t, axis=1) # 정답 숫자
acc = np.sum(y==t) / x.shape[0]
return acc
# 4장에서 구현한 기울기 구하는 함수
def numerical_gradient( self, x, t):
loss_W = lambda W : self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient( loss_W , self.params['W1'])
grads['b1'] = numerical_gradient( loss_W, self.params['b1'])
grads['W2'] = numerical_gradient( loss_W, self.params['W2'])
grads['b2'] = numerical_gradient( loss_W, self.params['b2'])
return grads
# 5장에서 배울 기울기 구하는 함수
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
da1 = np.dot(dy, W2.T)
dz1 = sigmoid_grad(a1) * da1
grads['W1'] = np.dot(x.T, dz1)
grads['b1'] = np.sum(dz1, axis=0)
return grads
# 1. 설계도로 제품을 만듭니다.
net = TwoLayerNet(weight__init_std = 0.0001)
#2. 필기체 데이터를 로드합니다.
from tensorflow.keras.datasets.mnist import load_data
(x_train, y_train), (x_test, y_test) = load_data(path = 'mnist.npz')
#3.훈련 데이터를 구성합니다.
x_train = x_train.reshape(60000,28*28)
x_train = x_train/255
#4.훈련 데이터의 정답데이터를 구성합니다.
y_train = to_categorical(y_train)
y_train = y_train.reshape(60000,10)
#5.테스트 데이터를 구성합니다.
x_test = x_test.reshape(10000,28*28)
x_test = x_test/255
#6.테스트 데이터의 정답데이터를 구성합니다.
y_test = to_categorical(y_test)
y_test = y_test.reshape(10000,10)
train_loss_list=[] # 오차값을 저장할 리스트
train_acc_list =[] # 훈련 데이터의 정확도를 저장할 리스트
test_acc_list = [] # 테스트 데이터의 정확도를 저장할 리스트
for i in range(600*40):
batch_mask = np.random.choice(60000, 100) # 0부터 60000까지의 숫자중에서 100개의 숫자를 랜덤으로 추출
x_batch = x_train[batch_mask] # 100개의 이미지 데이터를 추출
t_batch = y_train[batch_mask] # 100개의 정답 데이터를 추출
grad = net.gradient(x_batch, t_batch)
for key in ('W1', 'b1', 'W2', 'b2'):
net.params[key] -= 0.1 * grad[key]
loss = net.loss(x_batch, t_batch)
if i % 600==0:
train_loss_list.append(loss)
train_acc = net.accuracy(x_train, y_train)
test_acc = net.accuracy(x_test, y_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc :" +str(train_acc) + ',' + str(test_acc))
print(train_acc_list)
print(test_acc_list)가중치 초기값 선정을 0.0001로 했을 때 아래와 같은 결과가 나옴
train acc, test acc :0.9669333333333333,0.9616
가중치 초기값 선정을 1000을 곱했을때 => 표준편차가 아주 큼. 극단으로 결과가 나뉨.
net = TwoLayerNet(weight__init_std = 10000)train acc, test acc :0.09715,0.1008학습이 전혀 되지 않은걸 확인할 수 있음.
그래서 가중치 초기값 선정이 매우 중요함
가중치 초기값 0.01을 했을 때
net = TwoLayerNet(weight__init_std = 0.01)train acc, test acc :0.9689833333333333,0.9626위와 같이 가중치 초기값이 학습 결과에 영향을 미친다는 것을 확인했습니다.
날코딩이 아닐때 즉, 텐서플로우로 할 때 적당한 가중치 초기값을 선정하는 방법은 무엇인가?
텐서플로우는 알아서 하니까 Xavier 나 He초기값을 설정할 수 있는데 날코딩은 아래의 공식을 적용해야함.
1. Xavier 초기값 선정

2. He 초기값 선정

혹시 학습이 잘 안될때 확인해봐야 하는 사항으로 가중치 초기값이 어떻게 설정되어 있는지 확인하면 됩니다.
2 배치정규화(batch normalization) - p210
가중치 초기값을 적당한 값으로 설정하면 각 층의 활성화 값의 분포가 적당히 퍼지는 효과를 보이는데 신경망이 깊어지고 학습이 반복되다 보면 각 층의 활성화 값의 분포가 정규성을 잃어버리는 현상이 발생하게 됨.

정규성을 잃어버리게 되는 것은 층이 깊어질수록 발생할 확률이 높음.
그래서 배치 정규화는 층 중간중간 배치 정규화 층을 추가해서 가중치값의 정규성을 강제로 유지시킴.

배치 단위로 신경망에 들어오는 데이터에 대한 학습 가중치에 대해서 정규성을 유지시키겠다는 것.
(언더피팅과 오버피팅 둘 다 효과 있음)

ㅇ배치정규화를 안썼을 때와 썼을 때의 코드 비교
1. 배치 정규화 안썼을 떄
#4. 모델 구성
model = Sequential()
model.add(Dense(50, activation = 'sigmoid')) #은닉층(1층)
model.add(Dense(50, activation = 'sigmoid')) #은닉층(2층)
model.add(Dense(10, activation = 'softmax')) #출력층2. 배치 정규화 썼을 때
#4. 모델 구성
model = Sequential()
model.add(Dense(50, activation = 'sigmoid')) #은닉층(1층)
model.add(BatchNormalization())
model.add(Dense(50, activation = 'sigmoid')) #은닉층(2층)
model.add(BatchNormalization())
model.add(Dense(10, activation = 'softmax')) #출력층
문제138. 배치 정규화를 썼을 때와 안썼을 때의 정확도의 차이를 실험하시오.
#배치정규화 안 썼을 때
# 1. 필요한 패키지 가져오는 코드
import tensorflow as tf # 텐써 플로우 2.0
from tensorflow.keras.datasets.mnist import load_data # 텐써플로우에 내장되어있는
# mnist 데이터를 가져온다.
from tensorflow.keras.models import Sequential # 모델을 구성하기 위한 모듈
from tensorflow.keras.layers import Dense # 완전 연결계층을 구성하기 위한 모듈
from tensorflow.keras.layers import Flatten
from tensorflow.keras.utils import to_categorical # one encoding 하는 모듈
tf.random.set_seed(777)
(x_train, y_train), (x_test, y_test) = load_data(path='mnist.npz') # mnist 데이터 로드
# 2. 정규화 진행
x_train = x_train/255
x_test = x_test/255
# 3. 정답 데이터를 준비한다.
# 하나의 숫자를 one hot encoding 한다. (예: 4 ---> 0 0 0 0 1 0 0 0 0 0 )
y_train = to_categorical(y_train) # 훈련 데이터의 라벨(정답)을 원핫 인코딩
y_test = to_categorical(y_test) # 테스트 데이터의 라벨(정답)을 원핫 인코딩
# 4. 모델 구성
model = Sequential()
model.add(Flatten(input_shape = (28,28)))
model.add(Dense(50, activation = 'sigmoid')) #은닉층(1층)
model.add(Dense(50, activation = 'sigmoid')) #은닉층(2층)
model.add(Dense(10, activation = 'softmax')) #출력층
# 5. 모델을 설정합니다. ( 경사하강법, 오차함수를 정의해줍니다. )
model.compile(optimizer='SGD',
loss = 'categorical_crossentropy',
metrics=['acc'])
#6. 모델을 훈련시킵니다.
history = model.fit(x_train, y_train,
epochs = 30, # 30에폭
batch_size = 100,
validation_data = (x_test,y_test))
# 7.모델을 평가합니다. (오차, 정확도가 출력됩니다.)
model.evaluate(x_test, y_test) #[0.3981786072254181, 0.8894000053405762]
#8. 시각화
train_acc_list = history.history['acc']
test_acc_list = history.history['val_acc']
import matplotlib.pyplot as plt
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label = 'train_acc')
plt.plot(x, test_acc_list, label = 'test_acc')
plt.ylim(0,1)
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.legend()
plt.show()#배치정규화 썼을 때
# 1. 필요한 패키지 가져오는 코드
import tensorflow as tf # 텐써 플로우 2.0
from tensorflow.keras.datasets.mnist import load_data # 텐써플로우에 내장되어있는
# mnist 데이터를 가져온다.
from tensorflow.keras.models import Sequential # 모델을 구성하기 위한 모듈
from tensorflow.keras.layers import Dense # 완전 연결계층을 구성하기 위한 모듈
from tensorflow.keras.layers import Flatten, BatchNormalization
from tensorflow.keras.utils import to_categorical # one encoding 하는 모듈
tf.random.set_seed(777)
(x_train, y_train), (x_test, y_test) = load_data(path='mnist.npz') # mnist 데이터 로드
# 2. 정규화 진행
x_train = x_train/255
x_test = x_test/255
# 3. 정답 데이터를 준비한다.
# 하나의 숫자를 one hot encoding 한다. (예: 4 ---> 0 0 0 0 1 0 0 0 0 0 )
y_train = to_categorical(y_train) # 훈련 데이터의 라벨(정답)을 원핫 인코딩
y_test = to_categorical(y_test) # 테스트 데이터의 라벨(정답)을 원핫 인코딩
# 4. 모델 구성 + 배치정규화
model = Sequential()
model.add(Flatten(input_shape = (28,28)))
model.add(Dense(50, activation = 'sigmoid')) #은닉층(1층)
model.add(BatchNormalization())
model.add(Dense(50, activation = 'sigmoid')) #은닉층(2층)
model.add(BatchNormalization())
model.add(Dense(10, activation = 'softmax')) #출력층
# 5. 모델을 설정합니다. ( 경사하강법, 오차함수를 정의해줍니다. )
model.compile(optimizer='SGD',
loss = 'categorical_crossentropy',
metrics=['acc'])
#6. 모델을 훈련시킵니다.
history = model.fit(x_train, y_train,
epochs = 30, # 30에폭
batch_size = 100,
validation_data = (x_test,y_test))
# 7.모델을 평가합니다. (오차, 정확도가 출력됩니다.)
model.evaluate(x_test, y_test) #[0.1426546722650528, 0.9571999907493591]
#8. 시각화
train_acc_list = history.history['acc']
test_acc_list = history.history['val_acc']
import matplotlib.pyplot as plt
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label = 'train_acc')
plt.plot(x, test_acc_list, label = 'test_acc')
plt.ylim(0,1)
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.legend()
plt.show()'Study > class note' 카테고리의 다른 글
| 딥러닝 / 오버피팅 방지(드롭아웃, L2규제) (0) | 2022.04.14 |
|---|---|
| 딥러닝 / 언더피팅 방지(경사하강법과 활성화 함수의 조합을 적절하게 조합하기) (0) | 2022.04.14 |
| 딥러닝 / 2층 신경망을 텐서 플로우로 구현 (0) | 2022.04.13 |
| 딥러닝 / 파이썬 날코딩으로 2층 신경망 전체 코드 구현 (0) | 2022.04.13 |
| 딥러닝 / 오차역전파, Affine 계층 구현 (0) | 2022.04.12 |



